
【题目】设点P是直线![]() 上一点,过点P分别作抛物线
上一点,过点P分别作抛物线![]() 的两条切线
的两条切线![]() ,其中A、B为切点.
,其中A、B为切点.
(1)若点A的坐标为![]() ,求点P的横坐标;
,求点P的横坐标;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由导数的几何意义,可先求直线切线![]() 的斜率
的斜率![]() ,由点斜式写出直线
,由点斜式写出直线![]() 方程,再由点
方程,再由点![]() 纵坐标为-2代入直线方程即可求解;
纵坐标为-2代入直线方程即可求解;
(2)设![]() ,分别表示出直线
,分别表示出直线![]() 的方程为
的方程为![]() ,同理得
,同理得![]() ,由两直线均过
,由两直线均过![]() 得
得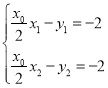 ,可推出直线方程为
,可推出直线方程为![]() ,联立抛物线方程
,联立抛物线方程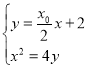 解出关于
解出关于![]() 的一元二次方程,结合弦长公式和点到直线距离公式表示出三角形面积公式为
的一元二次方程,结合弦长公式和点到直线距离公式表示出三角形面积公式为![]() ,即可求解
,即可求解![]() ,进而求解弦长
,进而求解弦长![]() ;还可设
;还可设![]() ,将
,将![]() 两点纵坐标结合抛物线代换,表示出直线
两点纵坐标结合抛物线代换,表示出直线![]() 的方程为
的方程为![]() ,同理直线
,同理直线![]() 的方程为
的方程为![]() ,联立解得
,联立解得![]() ,故
,故![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立
,联立 ,推出参数
,推出参数![]() ,后续求解步骤同前一种解法
,后续求解步骤同前一种解法
(1)由![]() ,所以
,所以![]() ,
,
因为![]() ,
,
由导数的几何意义知,切线![]() 的斜率
的斜率![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
又因为点P为直线![]() 与直线
与直线![]() 的公共点,
的公共点,
联立![]() 与
与![]() ,可得P点横坐标为
,可得P点横坐标为![]() .
.
(2)法一:不妨设![]() ,
,
由(1)可知![]() ,即直线
,即直线![]() 的方程为
的方程为![]() ,
,
即![]() ,同理可得
,同理可得![]()
因为切线![]() 均过点
均过点![]() ,所以
,所以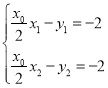 ,
,
所以![]() 为方程
为方程![]() 的两组解,
的两组解,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]()
联立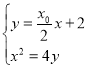 ,可得
,可得![]() ,显然
,显然![]() ,
,
由韦达定理得,![]() ,
,
所以 ,
,
又因为点P到直线![]() 的距离
的距离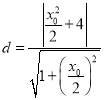 ,
,
所以 ,
,
解得![]() ,所以
,所以![]() .
.
法二:不妨设![]() ,由(1)可知直线
,由(1)可知直线![]() 的方程为
的方程为![]() ,
,
同理,直线![]() 的方程为
的方程为![]() ,
,
联立解得![]() ,
,
又点P在直线![]() ,所以
,所以![]() ,
,
设直线![]() 的方程为
的方程为![]() ,联立
,联立 ,可得
,可得![]() ,
,
由韦达定理得![]() ,
,
可得![]() ,
,
所以![]() ,
,
又因为点P到直线![]() 的距离为
的距离为 ,
,
所以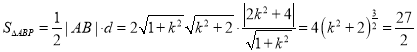 ,
,
解得![]() ,所以
,所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知二面角α﹣l﹣β为60°,在其内部取点A,在半平面α,β内分别取点B,C.若点A到棱l的距离为1,则△ABC的周长的最小值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
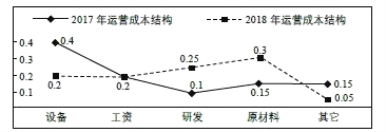
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面多边形![]() 中,四边形
中,四边形![]() 是边长为2的正方形,四边形
是边长为2的正方形,四边形![]() 为等腰梯形,
为等腰梯形,![]() 为
为![]() 的中点,
的中点,![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折叠,使平面
折叠,使平面![]() 平面
平面![]() .
.
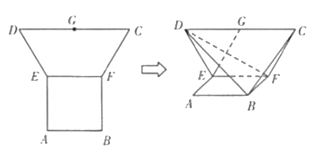
(1)求证:![]() 面
面![]() ;
;
(2)求![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九世纪末,法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”、“随机端点”、“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设A为圆O上一个定点,在圆周上随机取一点B,连接AB,所得弦长AB大于圆O的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:![]() ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
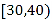
(1)现从年龄在![]() 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用![]() 表示年龄在
表示年龄在![]() 内的人数,求
内的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有![]() 名市民的年龄在
名市民的年龄在![]() 的概率为
的概率为![]() .当
.当![]() 最大时,求
最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
这三个条件中任选一个,补充在下面问题中的横线上,并解答相应的问题.
在![]() 中,内角A,B,C的对边分别为a,b,c,且满足________________,
中,内角A,B,C的对边分别为a,b,c,且满足________________,![]()
![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com