
分析 (1)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间,
(2)先求出当直线和y=lnx相切时a的取值,然后进行讨论求解即可.
解答  解:(1)若ax>lnx恒成立,
解:(1)若ax>lnx恒成立,
则a>$\frac{lnx}{x}$,在x>0时恒成立,
设h(x)=$\frac{lnx}{x}$,
则h′(x)=$\frac{\frac{1}{x}•x-lnx}{{x}^{2}}$=$\frac{1-lnx}{x}$,
由h′(x)>0得1-lnx>0,即lnx<1,得0<x<e,
由h′(x)<0得1-lnx<0,即lnx>1,得x>e,
即当x=e时,函数h(x)取得极大值同时也是最大值h(e)=$\frac{lne}{e}$=$\frac{1}{e}$.
即a>$\frac{1}{e}$.
(2)设f(x)=lnx,g(x)=ax,(x>0),
则f′(x)=$\frac{1}{x}$,当g(x)与f(x)相切时,设切点为(m,lnm),
则切线斜率k=$\frac{1}{m}$,
则过原点且与f(x)相切的切线方程为y-lnm=$\frac{1}{m}$(x-m)=$\frac{1}{m}$x-1,
即y=$\frac{1}{m}$x-1+lnm,
∵g(x)=ax,
∴$\left\{\begin{array}{l}{\frac{1}{m}=a}\\{-1+lnm=0}\end{array}\right.$,得m=e,a=$\frac{1}{e}$.
即当a>$\frac{1}{e}$时,ax>lnx恒成立.
当a=$\frac{1}{e}$时,当x0≥$\frac{1}{e}$时,
要使ax>lnx恒成立.得当x>x0时,ax>lnx恒成立.
当0<a<$\frac{1}{e}$时,f(x)与g(x)有两个不同的交点,不妨设较大的根为x1,当x0≥x1时,
当x>x0时,ax>lnx恒成立.
∴?a>0,?x0∈R,使得当x>x0时,ax>lnx恒成立.
点评 本题主要考查不等式恒成立问题,构造函数求函数的导数,利用导数是解决本题的关键.综合考查学生的运算和推理能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:解答题
等腰直角三角形斜边所在直线的方程是3x-y=0,一条直角边所在的直线l的斜率为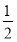 ,且经过点(4,-2),且此三角形的面积为10,求此直角三角形的直角顶点的坐标.
,且经过点(4,-2),且此三角形的面积为10,求此直角三角形的直角顶点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\sqrt{3}$,+∞) | B. | [3,+∞) | C. | (3,+∞) | D. | [9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
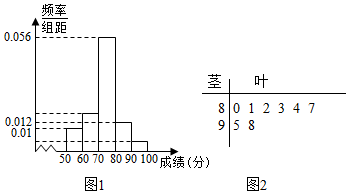
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com