
在平面直角坐标系中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图所示).
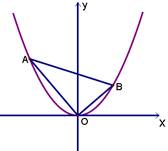
(Ⅰ)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
(Ⅰ)重心为G的轨迹方程为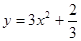
(Ⅱ)△AOB的面积存在最小值,最小值是1。
【解析】试题分析:(I)设△AOB的重心为G(x,y),A(x1,y1),B(x2,y2),则 (1)
(1)
∵OA⊥OB ∴ ,即
,即 ,(2)
,(2)
又点A,B在抛物线上,有 ,代入(2)化简得
,代入(2)化简得
∴
所以重心为G的轨迹方程为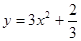
(2)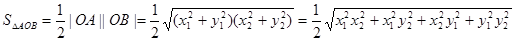
由(I)得
当且仅当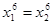 即
即 时,等号成立。
时,等号成立。
所以△AOB的面积存在最小值,最小值是1。
考点:本题主要考查了轨迹方程的求法、重心定理的应用及基本不等式的应用。
点评:本题综合性强既考查了学生的计算能力,又兼顾了知识的综合应用。(1)中给的是A、B的条件,要求重心G的轨迹方程,先化简A、B的关系式,再利用重心定理找到G点坐标与AB坐标的关系,化简出G的轨迹方程;(2)在求最值时。常用求导和基本不等式来求,本题中具备 为定值这一条件,所以选择用基本不等式求解,注意等号成立的条件的应用。
为定值这一条件,所以选择用基本不等式求解,注意等号成立的条件的应用。


科目:高中数学 来源: 题型:
| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com