
分析 先求出其导函数,把x=1代入,求出切线的斜率,进而得到切线方程,找到切线与y轴的交点的纵坐标的表达式,即可求出结论.
解答 解:因为y=xn+1,
故y′=(n+1)xn,
所以x=1时,y′=n+1,
则直线方程为y-1=(n+1)(x-1),
令x=0,则y=1-(n+1)=-n,
故切线与y轴的交点为( 0,-n),
即有bn=2yn=-2n,
则b1•b2•…b2010=(-2)×(-4)×…×(-4020)
=22010•2010!.
故答案为:22010•2010!.
点评 当题目中遇到求曲线C在点A(m,n)的切线方程时,其处理步骤为:①判断A点是否在C上②求出C对应函数的导函数③求出过A点的切线的斜率④代入点斜式方程,求出直线的方程.同时考查运算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
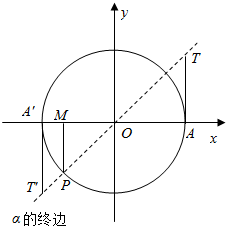 如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )
如图所示,P是角α得终边与单位圆的交点,PM⊥x轴于M,AT和A′T′均是单位圆的切线,则角α的( )| A. | 正弦值是PM,正切线是A′T′ | B. | 正弦值是MP,正切线是A′T′ | ||
| C. | 正弦值是MP,正切线是AT | D. | 正弦值是PM,正切线是AT |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=1 | B. | x=-1 | C. | y=1 | D. | y=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{10}$,1)∪(1,10) | B. | ($\frac{1}{10}$,1)∪(2,10) | C. | ($\frac{1}{10}$,10) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7m/s | B. | 6m/s | C. | 2m/s | D. | 1m/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com