
分析 (1)若命题p为真命题,则$\left\{\begin{array}{l}m+1>0\\ m-1<0\end{array}\right.$,解得实数m的取值范围;
(2)若“p∧q”为假命题,“p∨q”为真命题,则命题p,q一真一假,进而可得实数m的取值范围.
解答 解:(1)∵方程$\frac{x^2}{m+1}+\frac{y^2}{m-1}=1$表示焦点在x轴上的双曲线,
∴$\left\{\begin{array}{l}m+1>0\\ m-1<0\end{array}\right.$,
即-1<m<1,…(4分)
∴若命题p为真命题,则实数m的取值范围是(-1,1)…(5分)
(2)若“p∧q”为假命题,“p∨q”为真命题,
则p,q为一个真命题,一个假命题,…(7分)
若关于x的方程x2+2mx+2m+3=0无实根,
则判别式△=4m2-4(2m+3)<0,…(8分)
即m2-2m-3<0,得-1<m<3.…(9分)
若p真q假,则$\left\{\begin{array}{l}-1<m<1\\ m≤-1,或m≥3\end{array}\right.$,此时无解,…(10分)
柔p假q真,则$\left\{\begin{array}{l}-1<m<3\\ m≤-1,或m≥1\end{array}\right.$,得1≤m<3,…(11分)
综上,实数m的取值范围是[1,3)…(12分)
点评 本题以命题的真假判断与应用为载体,考查了双曲线的标准方程,方程根的存在性及个数判断,难度中档.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°,
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{10}$+y2=1 | B. | $\frac{{x}^{2}}{19}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
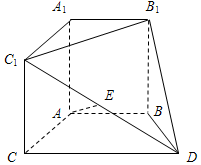 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com