Question

已知函数f（x）=x²+t的图象与函数g（x）=ln|x|的图象有四个交点，则实数t的取值范围为________．

Answer 1

（-∞，--ln2）
分析：利用导数求出求出这两个函数的图象在（0，+∞）上相切时切点的横坐标，再由题意可得f（）＜g（），由此求得实数m的取值范围．
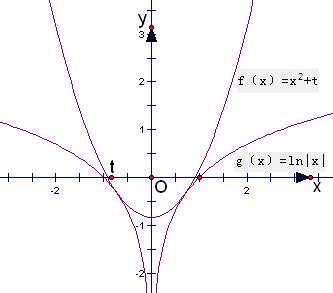
解答：解：由于函数f（x）和函数g（x）都是偶函数，图象关于y轴对称，故当这两个函数在（0，+∞）上有2个交点时，函数f（x）=x²+t的图象与函数g（x）=ln|x|的图象有四个交点．
当x＞0时，令 h（x）=f（x）-g（x）=x²+t-lnx，则 h′（x）=2x-．
令h′（x）=0可得x=，故这两个函数的图象在（0，+∞）上相切时切点的横坐标为x=．
当x=时，f（x）=+t，g（x）=ln =-ln2，
函数f（x）=x²+t的图象与函数g（x）=ln|x|的图象有四个交点，应有 +t＜-ln2，
由此可得 t＜--ln2，故实数m的取值范围为 （-∞，--ln2），
故答案为 （-∞，--ln2）．
点评：本题考查了根的存在性及根的个数判断，以及函数与方程的思想，求出这两个函数的图象在（0，+∞）上相切时切点的横坐标为x=，是解题的关键，属于中档题．