
已知函数f(x)=ax-![]() -2lnx
-2lnx
(1)若函数f(x)在其定义域内为递增函数,求实数a的取值函数;
(2)若函数f(x)的图像在x=1处的切线的斜率为0,并且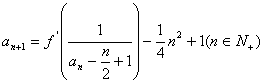 .①若a1≥3,试证明
.①若a1≥3,试证明![]() ;
;
②若a1=4,试比较![]() 与
与![]() 的大小,并说明你的理由。
的大小,并说明你的理由。
解:(1)由f(x)可得f![]() (x)=
(x)=![]() , ∴f
, ∴f![]() (x)≥0在(0,+∞)恒成立
(x)≥0在(0,+∞)恒成立
∴ax2-2x+a≥0恒成立, ∴ a≥![]() 在(0,+∞)恒成立
在(0,+∞)恒成立
故a≥1--------------------------------------6
(2)∵函数f(x)的图像在x=1处的切线的斜率为0
∴f![]() (1)=0,即a+a-2=0,解得a=1
(1)=0,即a+a-2=0,解得a=1
∴f![]() (x)=
(x)=![]()
∴
![]() =
=![]()
=![]() ---------------------------8
---------------------------8
① 用数学归纳法证明:
(ⅰ)当n=1时,a1≥3=1+2,不等式成立。
(ⅱ)假设n=k时,不等式成立,即ak≥k+2,那么ak-k≥2>0,
∴ak+1=ak(ak-k)+1≥2(k+2)+1=(k+3)+k+2>k+3,
综上述可知,对于所有n≥1都有![]()
②![]() 及①知对于k≥2,有
及①知对于k≥2,有![]()
∴![]() ------------------------------10
------------------------------10
∵ a1=4,∴![]() ,于是当k≥2时,
,于是当k≥2时,![]() ,
,
∴![]() ≤
≤![]()
=![]() <
<![]()


科目:高中数学 来源: 题型:
| 1 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x-1) | x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2x-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com