练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．函数f（x）=$\frac{x-1}{x+1}$的单调递增区间是（-∞，-1）和（-1，+∞）．．

    分析 利用分离常数法将函数化简，可得函数为反函数的类型，根据反函数的性质可得单调性．

    解答 解：由题意：∵函数f（x）=$\frac{x-1}{x+1}$=$\frac{x+1-2}{x+1}=1-\frac{2}{x+1}$，
    ∵$\frac{-2}{x+1}$在定义域（-∞，-1）和（-1，+∞）上是单调增函数．
    故得函数f（x）的单调递增区间为（-∞，-1）和（-1，+∞）．
    故答案为（-∞，-1）和（-1，+∞）．

    点评 本题考查了函数的化简能力转化成耳麦熟悉的基本函数类型，利用了分离常数法．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=x2+ax-3，g（x）=$\frac{klnx}{x}$，当a=2时，f（x）与g（x）的图象在x=1处的切线相同．
    （1）求k的值；
    （2）令F（x）=f（x）-g（x），若F（x）存在零点，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．下列事件为必然事件的是（　　）
    A．在一标准大气压下，20℃的纯水结冰
    B．平时的百分制考试中，小白的考试成绩为100分
    C．抛一枚硬币，落下后正面朝上
    D．边长为a，b的长方形面积为ab

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．给出下列四个命题：
    ①函数f（x）=loga（2x-1）-1的图象过定点（1，0）；
    ②已知函数f（x）是定义在R上的偶函数，当x≤0时，f（x）=x（x+1），则f（x）的解析式为f（x）=x2-|x|；
    ③函数y=$\frac{1}{|x|-1}$的图象可由函数y=$\frac{1}{|x|}$图象向右平移一个单位得到；
    ④函数y=$\frac{1}{|x|-1}$图象上的点到（0，1）距离的最小值是$\sqrt{3}$．
    其中所有正确命题的序号是②④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．如图，在直四棱柱ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，E，F分别为线段DD1，BD的中点．
    （1）求证：EF∥平面ABC1D1；
    （2）四棱柱ABCD-A1B1C1D1的外接球的表面积为16π，求异面直线EF与BC所成的角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设函数f（x）=x2-2ax+2（x∈[-1，1]）的最小值为g（a），求g（a）的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知圆C：x2+y2+Dx+Ey+F=0的圆心在第二象限，半径为$\sqrt{2}$，且圆C与直线3x+4y=0及y轴都相切．
    （1）求D、E、F；
    （2）若直线x-y+2$\sqrt{2}$=0与圆C交于A、B两点，求|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

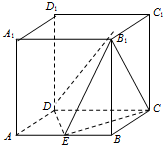    13．如图，在正方体ABCD-A1B1C1D1中，E为AB上一点．
    （1）求BD和平面B1CD所成的角；
    （2）当E点为AB中点，求锐二面角E-B1C-D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

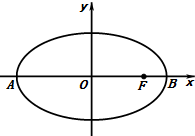    14．在平面直角坐标系xOy中，如图所示，已知椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的左、右顶点分别为A，B，右焦点为F．设过点T（t，m）的直线TA，TB与此椭圆分别交于点M（x1，y1），N（x2，y2），其中m＞0，y1＞0，y2＜0．
    （Ⅰ）设动点P满足：|PF|2-|PB|2=4，求点P的轨迹；
    （Ⅱ）设${x_1}=2，{x_2}=\frac{1}{3}$，求点T的坐标；
    （Ⅲ）设t=9，求证：直线MN必过x轴上的一定点（其坐标与m无关），并求出该定点的坐标．

    查看答案和解析>>

    同步练习册答案