
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)(
(天)(![]() )的关系如图所示
)的关系如图所示
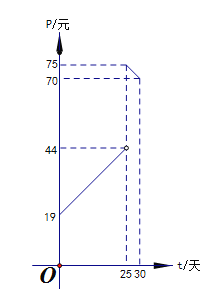
(1)写出销售价格![]() (元)和时间
(元)和时间![]() (天)的函数解析式;
(天)的函数解析式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系是
(天)的函数关系是![]() (
(![]() ,
,![]() ),求该商品的日销售金额
),求该商品的日销售金额![]() (元)与时间
(元)与时间![]() (天)的函数解析式;
(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,焦距为2,抛物线
,焦距为2,抛物线![]() 的准线经过C的左焦点F.
的准线经过C的左焦点F.
(1)求C与M的方程;
(2)直线l经过C的上顶点且l与M交于P,Q两点,直线FP,FQ与M分别交于点D(异于点P),E(异于点Q),证明:直线DE的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量![]() (万只)与时间
(万只)与时间![]() (年)(其中
(年)(其中![]() )的关系为
)的关系为![]() .为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值
.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值![]() (其中
(其中![]() 为常数,且
为常数,且![]() )来进行生态环境分析.
)来进行生态环境分析.
(1)当![]() 时,求比值
时,求比值![]() 取最小值时
取最小值时![]() 的值;
的值;
(2)经过调查,环保部门发现:当比值![]() 不超过
不超过![]() 时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数
时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底,
为自然对数的底, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知扇形![]() 是一个观光区的平面示意图,其中扇形半径为10米,
是一个观光区的平面示意图,其中扇形半径为10米,![]() ,为了便于游客观光和旅游,提出以下两种设计方案:
,为了便于游客观光和旅游,提出以下两种设计方案:
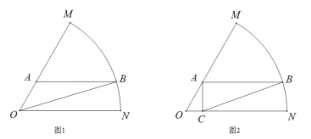
(1)如图1,拟在观光区内规划一条三角形![]() 形状的道路,道路的一个顶点
形状的道路,道路的一个顶点![]() 在弧
在弧![]() 上,另一顶点
上,另一顶点![]() 在半径
在半径![]() 上,且
上,且![]() ,求
,求![]() 周长的最大值;
周长的最大值;
(2)如图2,拟在观光区内规划一个三角形区域种植花卉,三角形花圃![]() 的一个顶点
的一个顶点![]() 在弧
在弧![]() 上,另两个顶点
上,另两个顶点![]()
![]() 在半径
在半径![]()
![]() 上,且
上,且![]() ,
,![]() ,求花圃
,求花圃![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,过焦点且与
,过焦点且与![]() 轴垂直的直线被椭圆
轴垂直的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知点![]() ,
,![]() ,过点
,过点![]() 的任意一条直线
的任意一条直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() (万元),若年产量不足
(万元),若年产量不足![]() 千件,
千件, ![]() 的图像是如图的抛物线,此时
的图像是如图的抛物线,此时![]() 的解集为
的解集为![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年产量不小于
,若年产量不小于![]() 千件,
千件, ![]() ,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
,每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完;
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
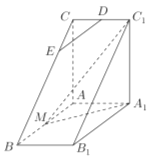
【题目】如图,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,△
的中点,△![]() 是等腰三角形,
是等腰三角形, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 上一点;
上一点;
(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求含有点
分成两个部分,求含有点![]() 的那部分体积;
的那部分体积;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: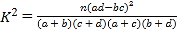 ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com