Question

判断下列函数在给定区间是否存在零点．
（1）f（x）=x²-3x-18，x∈[1，8]；
（2）f（x）=log₂（x+2）-x，x∈[1，3]．

Answer 1

解：（1）令f（x）=0得x²-3x-18=0，x∈[1，8]
'∴（x-6）（x+3）=0，
∴x=6∈[1，8]，x=-3∉[1，8]，
故f（x）=x²-3x-18，x∈[1，8]存在零点．

（2）方法一：
∵f（1）=log₂3-1＞log₂2-1=0，f（3）=log₂5-3＜log₂8-3=0，
∴f（1）•f（3）＜0，
故f（x）=log₂（x+2）-x，x∈[1，3]存在零点
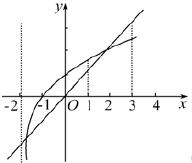
方法二：设y=log₂（x+2），y=x，在同一直角坐标系中画出它们的图象，
从图象中可以看出当1≤x≤3时，两图象有一个交点，
因此f（x）=log₂（x+2）-x，x∈[1，3]存在零点．
分析：利用函数零点的存在定理确定出零点是否存在，或者通过解方程、数形结合解出其零点，
（1）可以利用零点的存在性定理或直接求出零点，
（2）可以利用零点的存在性定理或利用两图象的交点来确定函数是否有零点．
点评：本题考查函数零点的确定方法，考查函数与方程的思想，考查学生的数形结合思想．也可根据连续函数零点的存在定理进行零点存在的判定．