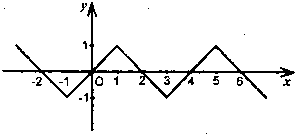
解:(Ⅰ)∵函数f(x)是奇函数,
∴f(-x)=-f(x).
令x=0,f(0)=-f(0),2f(0)=0,
∴f(0)=0.…
(Ⅱ)证:∵函数f(x)是奇函数,
∴f(x)=-f(-x)…(1)
又f(x)关于直线x=1对称,
∴f(1+x)=f(1-x).
在(1)中的x换成x+1,即f(1+x)=-f(-1-x),
即f(1-x)=-f(-1-x)…(2)
在(2)中,将1-x换成x,即f(x)=-f(-2+x)…(3)
在(3)中,将x换成2+x,即f(2+x)=-f(x)…(4)
由(3)、(4)得:f(-2+x)=f(2+x).
再将x-2换成x,得:f(x)=f(x+4).
∴f(x)是以4为周期的周期函数.…
(Ⅲ)设-1≤x<0时,则0<-x≤1,所以f(-x)=-x.
又f(-x)=-f(x),所以f(x)=x,又f(0)=0,
所以,当-1≤x≤1时,f(x)=x.
当1<x<3时,-3<-x<-1,则-1<2-x<1.
所以f(2-x)=2-x,而函数f(x)的图象关于直线x=1对称,
所以f(2-x)=f(x),即f(x)=2-x.
所以x∈[-1,3]时,函数f(x)的解析式为:
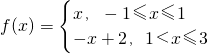
再由f(x)是以4为一个周期的周期函数,
从而有x∈R时,函数f(x)的解析式为:
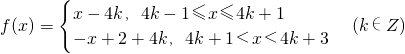
,
函数f(x)一个周期的图象如图所示.…
分析:(I)由函数f(x)是奇函数,所以f(-x)=-f(x),令x=0 可得f(0)=0.
(II)根据f(-x)=-f(x),再由函数f(x)的图象关于直线x=1对称,f(-x)=f(2+x),可得f(2+x)=-f(x),从而得到 f(4+x)=f(x),从而结论成立.
(III)由条件求出当-1≤x≤1时f(x)=x,当1<x<3时,则-1<2-x<1,可得f(2-x)=2-x,而函数f(x)的图象关于直线x=1对称,所以f(2-x)=f(x),即f(x)=2-x.从而得到f(x)在一个周期内的解析式,从而得到f(x)在定义域内的解析式,从而画出函数的图象.
点评:本题主要考查函数的奇偶性和周期性的综合应用,求函数解析式得方法,求出1<x<3时,函数解析式为f(x)=2-x,是解题的关键.

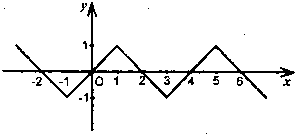 解:(Ⅰ)∵函数f(x)是奇函数,
解:(Ⅰ)∵函数f(x)是奇函数,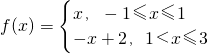
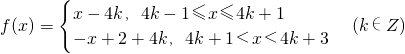 ,
,

 已知函数f(x)=x+
已知函数f(x)=x+