
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示. 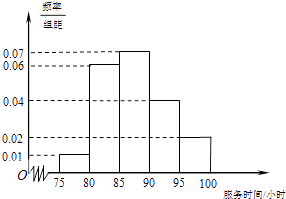
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
【答案】
(1)解:由题意可知,
参加社区服务在时间段[90,95)的学生人数为20×0.04×5=4(人),
参加社区服务在时间段[95,100]的学生人数为20×0.02×5=2(人).
所以参加社区服务时间不少于90小时的学生人数为 4+2=6(人).
(2)解:设所选学生的服务时间在同一时间段内为事件A.
由(1)可知,
参加社区服务在时间段[90,95)的学生有4人,记为a,b,c,d;
参加社区服务在时间段[95,100]的学生有2人,记为A,B.
从这6人中任意选取2人有ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB
共15种情况.
事件A包括ab,ac,ad,bc,bd,cd,AB共7种情况.
所以所选学生的服务时间在同一时间段内的概率 ![]()
【解析】(1)利用频率分布直方图,求出频率,进而根据频数=频率×样本容量,得到答案;(2)先计算从参加社区服务时间不少于90小时的学生中任意选取2人的情况总数,再计算所选学生的参加社区服务时间在同一时间段内的情况数,代入古典概型概率计算公式,可得答案.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a3=3,S11=0.
(1)求数列{an}的通项公式;
(2)当n为何值时,Sn最大,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的正三角形中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 上的点,且满足
上的点,且满足![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() .(如图2)
.(如图2)
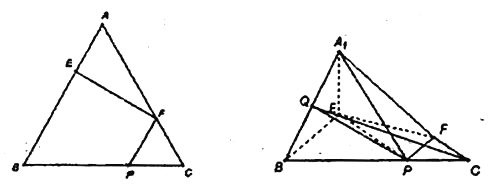
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求![]() 与平面
与平面![]() 所成角的正切.
所成角的正切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.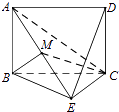
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是边长为1的正方形,PA⊥平面ABCD,N是PC的中点.
(Ⅰ)若PA=1,求二面角B﹣PC﹣D的大小;
(Ⅱ)求AN与平面PCD所成角的正弦值的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则下面结论中错误的一个是( ) 
A.甲的极差是29
B.乙的众数是21
C.甲罚球命中率比乙高
D.甲的中位数是24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中, ![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(I)求证: ![]() 平面
平面![]() ;
;
(II)当直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() 时,求证:
时,求证: ![]() ;
;
(III)在(II)的条件下,求异面直线![]() 与
与![]() 所成的余弦值.
所成的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com