
【题目】郴州某超市计划按月订购一种饮料,每天进货量相同,进货成本每瓶6元,售价每瓶8元,未售出的饮料降价处理,以每瓶3元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种饮料一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种饮料的利润为Y(单位:元),当六月份这种饮料一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
【答案】(2)详见解析;(2)![]() 时,
时,![]() 的数学期望达到最大值,最大值为
的数学期望达到最大值,最大值为![]() 元.
元.
【解析】
(1)由题意知![]() 的可能取值为200,300,500,分别求出相应的概率,由此能求出
的可能取值为200,300,500,分别求出相应的概率,由此能求出![]() 的分布列.
的分布列.
(2)由题意知这种酸奶一天的需求量至多为500瓶,至少为200瓶,只需考虑![]() ,根据
,根据![]() 和
和![]() 分类讨论,能得到当
分类讨论,能得到当![]() 时,
时,![]() 最大值为520元.
最大值为520元.
解:(1)由题意知![]() 的可能取值为200,300,500,
的可能取值为200,300,500,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的分布列为:
的分布列为:
| 200 | 300 | 500 |
| 0.2 | 0.4 | 0.4 |
(2)由题意知这种酸奶一天的需求量至多为500瓶,至少为200瓶,
![]() 只需考虑
只需考虑
当![]() 时,
时,
若最高气温不低于25,则![]() ;
;
若最高气温位于区间![]() ,
,![]() ,则
,则![]() ;
;
若最高气温低于20,则![]() ,
,
![]() ,
,
当![]() 时,
时,
若最高气温不低于20,则![]() ,
,
若最高气温低于20,则![]() ,
,
![]() .
.
![]() 时,
时,![]() 的数学期望达到最大值,最大值为
的数学期望达到最大值,最大值为![]() 元.
元.


科目:高中数学 来源: 题型:
【题目】下列命题中,正确的个数是( )
①直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
②![]() 为异面直线,则过
为异面直线,则过![]() 且与
且与![]() 平行的平面有且仅有一个;
平行的平面有且仅有一个;
③直四棱柱是直平行六面体;
④两相邻侧面所成角相等的棱锥是正棱锥.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求证:![]() ,并由
,并由![]() 推导
推导![]() 的值;
的值;
(2)若数列![]() 共有
共有![]() 项,前
项,前![]() 项的和为
项的和为![]() ,其后的
,其后的![]() 项的和为
项的和为![]() ,再其后的
,再其后的![]() 项的和为
项的和为![]() ,求
,求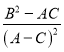 的比值.
的比值.
(3)若数列![]() 的前
的前![]() 项,前
项,前![]() 项、前
项、前![]() 项的和分别为
项的和分别为![]() ,试用含字母
,试用含字母![]() 的式子来表示
的式子来表示![]() (即
(即![]() ,且不含字母
,且不含字母![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义符号函数![]() ,已知函数
,已知函数![]() .
.
(1)已知![]() ,求实数
,求实数![]() 的取值集合;
的取值集合;
(2)当![]() 时,
时,![]() 在区间
在区间![]() 上有唯一零点,求
上有唯一零点,求![]() 的取值集合;
的取值集合;
(3)已知![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求正实数
,求正实数![]() 的取值集合;
的取值集合;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孔子曰:温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系,某校志愿者展开了积极的调查活动:从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查,所得信息如下:
数学成绩优秀(人数) | 数学成绩合格(人数) | |
及时复习(人数) | 20 | 4 |
不及时复习(人数) | 10 | 6 |
(1)张军是640名学生中的一名,他被抽中进行问卷调查的概率是多少(用分数作答);
(2)根据以上数据,运用独立性检验的基本思想,研究数学成绩与及时复习的相关性.
参考公式: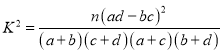 ,其中
,其中![]() 为样本容量
为样本容量
临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使得
,使得![]() 为
为![]() 上的奇函数,则称
上的奇函数,则称![]() 是位差值为
是位差值为![]() 的“位差奇函数”.
的“位差奇函数”.
(1)判断函数![]() 和
和![]() 是否为位差奇函数?说明理由;
是否为位差奇函数?说明理由;
(2)若![]() 是位差值为
是位差值为![]() 的位差奇函数,求
的位差奇函数,求![]() 的值;
的值;
(3)若![]() 对任意属于区间
对任意属于区间![]() 中的
中的![]() 都不是位差奇函数,求实数
都不是位差奇函数,求实数![]() 、
、![]() 满足的条件.
满足的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com