
【题目】设定义在R上的函数![]() ,当
,当![]() 时,
时,![]() 取极大值
取极大值![]() ,且函数
,且函数![]() 的图象关于原点对称.
的图象关于原点对称.
(1)求![]() 的表达式;
的表达式;
(2)试在函数![]() 的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在
的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在![]() 上;
上;
(3)设![]() ,
,![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的长轴长为4.
的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AB∥CD,BC⊥CD,侧面PAB为等边三角形,AB=BC=2CD=2.
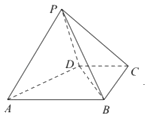
(Ⅰ)证明:AB⊥PD;
(Ⅱ)若PD=2,求直线PC与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区随着经济的发展,居民收入逐年增长,银行储蓄连年增长,下表是该地区某银行连续五年的储蓄存款(年底结算):
年份 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
为方便研究,工作人员对上表的数据做了如下处理:![]() ,
,![]() 得到下表:
得到下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的线性回归方程,并用所求回归方程预测
的线性回归方程,并用所求回归方程预测![]() 年底,该地储蓄存款额可达多少?
年底,该地储蓄存款额可达多少?
(附:参考公式![]() ,其中
,其中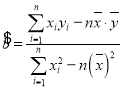 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com