
【题目】《中国谜语大会》是中央电视台科教频道的一档集文化、益智、娱乐为一体的大型电视竞猜节目,目的是为弘扬中国传统文化、丰富群众文化生活.为选拔选手参加“中国谜语大会”,某地区举行了一次“谜语大赛”活动.为了了解本次竞赛选手的成绩情况,从中抽取了部分选手的分数(得分取正整数,满分为100分)作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100)的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60),[90,100)的数据). 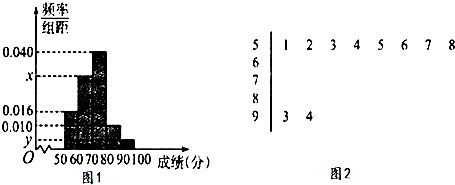
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)分数在[80,90)的学生中,男生有2人,现从该组抽取三人“座谈”,求至少有两名女生的概率.
【答案】
(1)解:由题意可知,样本容量 ![]() ,
,
故 ![]() ,
,
∴x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030.
∴n=50,x=0.030,y=0.004;
(2)解:分数在[80,90)的学生共有5人,由题意知,其中男生2人,女生3人,
分别设编号为b1,b2和a1,a2,a3,
则从该组抽取三人“座谈”包含的基本事件:
(a1,a2,a3),(a1,a2,b1),(a1,a3,b1),(a2,a3,b1),(a1,a2,b2),
(a1,a3,b2),(a2,a3,b2),(b1,b2,a1 ),(b1,b2,a2),(b1,b2,a3),共计10个,
记事件A“至少有两名女生”,则事件A包含的基本事件:
(a1,a2,a3),(a1,a2,b1),(a1,a3,b1),(a2,a3,b1),(a1,a2,b2),
(a1,a3,b2),(a2,a3,b2),共计7个.
所以,至少有两名女生的概率为P(A)= ![]()
【解析】(1)求出样本容量,从而求出x,y的值即可;(2)男生2人,女生3人,分别设编号为b1 , b2和a1 , a2 , a3 , 列出从该组抽取三人“座谈”包含的基本事件,记事件A“至少有两名女生”,列出事件A包含的基本事件,从而求出满足条件的概率即可.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】【2017南通一模19】已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() ,证明:函数
,证明:函数![]() 有且只有一个零点;
有且只有一个零点;
(3)若函数![]() 又两个零点,求实数
又两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x2﹣1|+x2+kx.
(1)若对于区间(0,+∞)内的任意x,总有f(x)≥0成立,求实数k的取值范围;
(2)若函数f(x)在区间(0,2)内有两个不同的零点x1 , x2 , 求:
①实数k的取值范围;
② ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有工程师6人,技术员12人,技工18人,要从这些人中抽取一个容量为n的样本.如果采用系统抽样和分层抽样方法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,求样本容量n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公比不为1的等比数列,a1=1,且a1 , a3 , a2成等差数列.
(1)求数列{an}的通项;
(2)若数列{an}的前n项和为Sn , 试求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B为曲线C:y=![]() 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM![]() BM,求直线AB的方程.
BM,求直线AB的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com