
【题目】设A,B为曲线C:y=![]() 上两点,A与B的横坐标之和为4.
上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM![]() BM,求直线AB的方程.
BM,求直线AB的方程.
【答案】(1)1(2)![]()
【解析】试题分析:(1)由直线斜率公式可得AB的斜率![]() ,再根据A与B的横坐标之和为4,得AB的斜率
,再根据A与B的横坐标之和为4,得AB的斜率![]() .(2)先根据导数几何意义得M点坐标,再根据直角三角形性质得
.(2)先根据导数几何意义得M点坐标,再根据直角三角形性质得![]() ,(AB的中点为N),设直线AB的方程为
,(AB的中点为N),设直线AB的方程为![]() ,与抛物线方程联立,利用两点间距离公式以及弦长公式可得关系式
,与抛物线方程联立,利用两点间距离公式以及弦长公式可得关系式![]() ,解得
,解得![]() .即得直线AB的方程为
.即得直线AB的方程为![]() .
.
试题解析:解:(1)设A(x1,y1),B(x2,y2),则![]() ,
, ![]() ,
, ![]() ,x1+x2=4,
,x1+x2=4,
于是直线AB的斜率![]() .
.
(2)由![]() ,得
,得![]() .
.
设M(x3,y3),由题设知![]() ,解得
,解得![]() ,于是M(2,1).
,于是M(2,1).
设直线AB的方程为![]() ,故线段AB的中点为N(2,2+m),|MN|=|m+1|.
,故线段AB的中点为N(2,2+m),|MN|=|m+1|.
将![]() 代入
代入![]() 得
得![]() .
.
当![]() ,即
,即![]() 时,
时, ![]() .
.
从而![]() .
.
由题设知![]() ,即
,即![]() ,解得
,解得![]() .
.
所以直线AB的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数![]() 在
在![]() 上的最大值为3时,求
上的最大值为3时,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数![]() ,
, ![]() 的图像与直线
的图像与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值.并求函数
的值.并求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 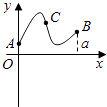
A.
B.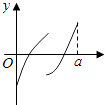
C.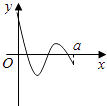
D.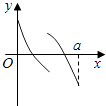
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
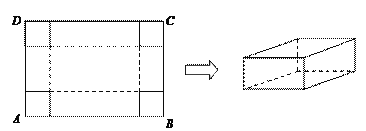
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家公司计划生产某种小型产品的月固定成本为1万元,每生产1万件需要再投入2万元,设该公司一个月内生产该小型产品x万件并全部销售完,每万件的销售收入为4﹣x万元,且每万件国家给予补助2e﹣ ![]() ﹣
﹣ ![]() 万元.(e为自然对数的底数,e是一个常数)
万元.(e为自然对数的底数,e是一个常数)
(1)写出月利润f(x)(万元)关于月产量x(万件)的函数解析式
(2)当月产量在[1,2e]万件时,求该公司在生产这种小型产品中所获得的月利润最大值(万元)及此时的月生成量值(万件).(注:月利润=月销售收入+月国家补助﹣月总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于R上的可导函数f(x),若a>b>1且有(x﹣1)f′(x)≥0,则必有( )
A.f(a)+f(b)<2f(1)
B.f(a)+f(b)≤2f(1)
C.f(a)+f(b)≥2f(1)
D.f(a)+f(b)>2f(1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+(1﹣a) x2﹣a(a+2)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是﹣3,求a,b的值;
(2)若函数f(x)在区间(﹣1,1)上不单调,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游景区的景点A处和B处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从A处出发,以50m/min的速度匀速步行,30min后到达B处,在B处停留20min后,再乘坐缆车回到A处.假设缆车匀速直线运动的速度为150m/mm.
(1)求该游客离景点A的距离y(m)关于出发后的时间x(mm)的函数解析式,并指出该函数的定义域;
(2)做出(1)中函数的图象,并求该游客离景点A的距离不小于1000m的总时长. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,即
,即![]() .
.
(1)若数列![]() 为首项为2016,公比为
为首项为2016,公比为![]() 的等比数列,
的等比数列,
①求![]() 的表达式;②当
的表达式;②当![]() 为何值时,
为何值时, ![]() 取得最大值;
取得最大值;
(2)当![]() 时,数列
时,数列![]() 都有
都有![]() 且
且![]() 成立,
成立,
求证: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com