
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 由∠AOB=120°,∠ACB=60°可知C在圆弧上运动,作出图形得出|$\overrightarrow{c}$|取得最大值时的位置,利用正弦定理求出外接圆直径.
解答 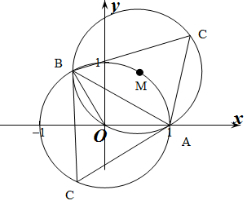 解:∵$\overrightarrow{a}•\overrightarrow{b}$=-1,∴$\overrightarrow{a},\overrightarrow{b}$的夹角为120°,
解:∵$\overrightarrow{a}•\overrightarrow{b}$=-1,∴$\overrightarrow{a},\overrightarrow{b}$的夹角为120°,
不妨设$\overrightarrow{OA}$=$\overrightarrow{a}$=(1,0),$\overrightarrow{OB}$=$\overrightarrow{b}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),$\overrightarrow{OC}$=$\overrightarrow{c}$,
则$\overrightarrow{CA}$=$\overrightarrow{a}-\overrightarrow{c}$,$\overrightarrow{CB}=\overrightarrow{b}-\overrightarrow{c}$,∵cos<$\overrightarrow{a}$-$\overrightarrow{c}$,$\overrightarrow{b}$-$\overrightarrow{c}$>=$\frac{1}{2}$,
∴∠ACB=60°,
∴C在圆x2+y2=1的优弧$\widehat{AB}$上或C在△AOB的外接圆的优弧$\widehat{AB}$上.
显然|$\overrightarrow{c}$|得最大值为△AOB的外接圆直径.
由正弦定理可知外接圆直径2R=$\frac{OA}{sin∠ABO}$=$\frac{1}{sin30°}$=2,
∴|$\overrightarrow{c}$|的最大值为2.
故选:A.
点评 本题考查了平面向量的运算,正弦定理得应用,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,e] | B. | [e-1-1,1] | C. | [1,e+1] | D. | [e-1-1,e+1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{3}{4},0}]$ | B. | $[{0,\frac{3}{4}}]$ | C. | $({-\frac{3}{4},0})$ | D. | $({0,\frac{3}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
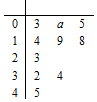 已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com