
| A�� | $2-\sqrt{2}$ | B�� | $\sqrt{2}$ | C�� | 2 | D�� | $2+\sqrt{2}$ |
���� ��$\overrightarrow a��\overrightarrow b$�ֱ���x����y���������ϵĵ�λ��������$\overrightarrow{a}$=��1��0����$\overrightarrow{b}$=��0��1����$\overrightarrow{a}$+$\overrightarrow{b}$=��1��1��������$\overrightarrow{c}$=��x��y���������$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$=��x-1��y-1��������|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{��x-1��}^{2}{+��y-1��}^{2}}$=2���ɵõ�C�Ĺ켣���ԣ�1��1��ΪԲ�ģ�2Ϊ�뾶��Բ�����Բ��M��1��1����ԭ��ľ���Ϊ|OM|=$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$���Ӷ��ɵô𰸣�
��� �⣺�����⣬��$\overrightarrow a��\overrightarrow b$�ֱ���x����y���������ϵĵ�λ������
��$\overrightarrow{a}$=��1��0����$\overrightarrow{b}$=��0��1����$\overrightarrow{a}$+$\overrightarrow{b}$=��1��1����
��$\overrightarrow{c}$=��x��y����
��$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$=��x-1��y-1����
��Ϊ|$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{��x-1��}^{2}{+��y-1��}^{2}}$=2��
���ԣ�x-1��2+��y-1��2=4��
��$\overrightarrow{c}$=$\overrightarrow{OC}$�У���C�Ĺ켣���ԣ�1��1��ΪԲ�ģ�2Ϊ�뾶��Բ��
Բ��M��1��1����ԭ��ľ���Ϊ|OM|=$\sqrt{{1}^{2}{+1}^{2}}$=$\sqrt{2}$��
$\overrightarrow{|c}$|max=$\sqrt{2}$+2��
��ѡ��D��
���� ���⿼��ƽ���������������������㣬��õ�C�Ĺ켣���ԣ�1��1��ΪԲ�ģ�2Ϊ�뾶��Բ�ǹؼ������������ӷ���������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��4x | B�� | y=��$\frac{1}{4}$x | C�� | y=��2x | D�� | y=��$\frac{1}{2}$x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -3��3 | C�� | -2��2 | D�� | -3��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q | B�� | ���Vp����q | C�� | p�ģ��Vq�� | D�� | p�ţ��Vq�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-3] | B�� | ��-�ޣ�2e] | C�� | ��-�ޣ�3] | D�� | ��-�ޣ�2e2+2e] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
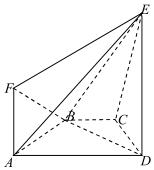 ��ͼ��ʾ����������ABCD�ĵ� A����60�㣬ֱ������ ADEF���ڵ�ƽ�洹ֱ��ƽ��ABCD����EDA=90�㣬��ED=AD=2AB=2AF��
��ͼ��ʾ����������ABCD�ĵ� A����60�㣬ֱ������ ADEF���ڵ�ƽ�洹ֱ��ƽ��ABCD����EDA=90�㣬��ED=AD=2AB=2AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-3] | B�� | ��-�ޣ�-3�� | C�� | ��-3��+�ޣ� | D�� | [-3��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com