
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-3,+∞) | D. | [-3,+∞) |
分析 依题意知,?x∈R,2ex-3≥k恒成立,构造函数g(x)=2ex-3,利用导数可知g(x)=2ex-3在R上单调递增,且x→-∞时,g(x)→-3,从而可得答案.
解答 解:∵$|\begin{array}{l}{{e}^{x}}&{3}\\{1}&{2}\end{array}|$=2ex-3≥k恒成立,
令g(x)=2ex-3,
则k≤g(x)min.
∵g′(x)=2ex>0,
∴g(x)=2ex-3在R上单调递增,
又x→-∞时,g(x)→-3,
∴k≤-3,
即实数k的取值范围是(-∞,-3],
故选:A.
点评 本题考查函数恒成立问题,考查构造函数思想与分离参数法的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
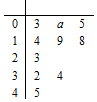 已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
| 印刷册数x(千册) | 2 | 3 | 4 | 5 | 8 | |
| 单册成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值$\widehat{{y}_{i}}$(1) | 2.4 | 2.1 | 1.6 | ||
| 残值$\widehat{{e}_{i}}$(1) | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值$\widehat{{y}_{i}}$(2) | 2.3 | 2 | 1.9 | ||
| 残值$\widehat{{e}_{i}}$(2) | 0.1 | 0 | 0 | |||
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 3 | C. | 8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{7}$ | D. | $\frac{3}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com