
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
分析 (Ⅰ)根据数学成绩优秀率是35%,构造关于m的方程,解方程可得m值,进而根据抽取样本容量为100,可得n值;
(Ⅱ)由题意m+n=35,且m≥10,n≥10,所以满足条件的(m,n)的基本事件总数及满足数学成绩优比良的人数少的基本事件个数,代入古典概型概率计算公式,可得答案.
解答 解:(Ⅰ)由题意得:$\frac{13+m+5}{100}$=$\frac{35}{100}$,解得:m=17,
由$\frac{5}{13+17+5}$=$\frac{1}{7}$,
故该生语文成绩为“及格”的概率是$\frac{1}{7}$;
(Ⅱ)由题意得:13+12+10+m+n+14+5+9+7=100,
故m+n=30,
记:数学成绩“优”比“良”的人数少为事件A,
∵m+n=30,m≥10,n≥10,
故满足条件的基本事件有:
(10,20),(11,19),(12,18),(13,17),
(14,16),(15,15),(16,14),(17,13),
(18,12),(19,11),(20,10)共11种,且每组出现都是等可能的,
其中事件A包含的基本事件有(10,20),(11,19),(12,18),(13,17),(14,16)共5种,
故P(A)=$\frac{5}{11}$.
点评 本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
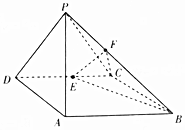 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,AB=DP=2$\sqrt{2}$,E为CD的中点,点F在线段PB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com