
分析 数列{an}的首项a1=1,且满足a2n+1=2a2n-1,可得数列{a2n-1}为等比数列,a2n-1=2n-1.a2n=a2n-1+1=2n-1+1,
因此a2n-1+a2n=2n+1,即可得出.
解答 解:数列{an}的首项a1=1,且满足a2n+1=2a2n-1,
可得数列{a2n-1}为等比数列,可得a2n-1=2n-1.
∴a2n=a2n-1+1=2n-1+1,
∴a2n-1+a2n=2n+1,
则S20=(a1+a2)+(a3+a4)+…+(a19+a20)
=21+22+…+210+10
=$\frac{2({2}^{10}-1)}{2-1}$+10=2056.
故答案为:2056.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、分组求和,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
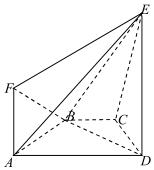 如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.
如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)<2016f($\root{3}{2016}$)<2017f($\root{3}{2017}$) | B. | 2017f($\root{3}{2017}$)<f(1)<2016f($\root{3}{2016}$) | ||
| C. | 2016f($\root{3}{2016}$)<f(1)<2017f($\root{3}{2017}$) | D. | 2017f($\root{3}{2017}$)<2016f($\root{3}{2016}$)<f(1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com