
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由$lo{g}_{\frac{1}{2}}$(x-1)>1,可得:$0<x-1<\frac{1}{2}$,解得集合A.由x2-2x-3>0,解得:x>3,或x<-1.即可判断出结论.
解答 解:由$lo{g}_{\frac{1}{2}}$(x-1)>1,可得:$0<x-1<\frac{1}{2}$,解得$1<x<\frac{3}{2}$,即集合A=$(1,\frac{3}{2})$.
由x2-2x-3>0,解得:x>3,或x<-1.即B(-∞,-1)∪(3,+∞).
则“x∈A”是“x∈B”的既不充分也不必要条件.
故选:D.
点评 本题考查了函数的单调性、不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
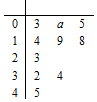 已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 3 | C. | 8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
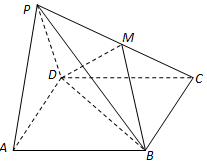 如图,在四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面BDM.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面BDM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{7}$ | D. | $\frac{3}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com