
���� ��1����Ȳ�����{an}�Ĺ���Ϊd���ȱ�����{bn}�Ĺ���Ϊq��������ã�$\left\{\begin{array}{l}{1+d={q}^{2}}\\{1+5d={q}^{4}}\end{array}\right.$�����d=0��3��������{an}��{bn}����������d��0��q��1���ɵ�an=3n-2��bn=2n-1������ͨ�ʽ���ɵó���
��2����Ȳ�����{cn}�Ĺ���Ϊd����a1����bn=3n������c1=1������cn=dn+1-d����Ϊb1=3��{cn}�е��������b1=cn����d��n-1��=2����n��4ʱ�����d=$\frac{2}{n-1}$��1�����������Ϊ��������b1=c3=3ʱ����b1=c2=3ʱ�����ɵó���
��3�����ڵȲ�����{an}��ֻ������a1�ʣ�1��q��������d=q-1����֤bn��bn+1֮������{an}������Ϊbn����֤������������n������$\left\{\begin{array}{l}{{b}_{n}��{a}_{{b}_{1}+{b}_{2}+��+{b}_{n-1}+1}}\\{{b}_{n+1}��{a}_{{b}_{1}+{b}_{2}+��+{b}_{n}}}\end{array}\right.$����������ͨ�ʽ���ɵó���
��� �⣺��1����Ȳ�����{an}�Ĺ���Ϊd���ȱ�����{bn}�Ĺ���Ϊq��
������ã�$\left\{\begin{array}{l}{1+d={q}^{2}}\\{1+5d={q}^{4}}\end{array}\right.$�����d=0��3��������{an}��{bn}����������
����d��0��q��1��
����d=3��q=2��
����an=3n-2��bn=2n-1������2�֣�
��Ϊa1=b1=1��a2=b3��a6=b5��b7��a20��
��c20=a17=49������4�֣�
��2����Ȳ�����{cn}�Ĺ���Ϊd����a1����bn=3n��
����c1=1������cn=dn+1-d��
��Ϊb1=3��{cn}�е��������b1=cn����d��n-1��=2��
��n��4ʱ�����d=$\frac{2}{n-1}$��1�����������Ϊ������������6�֣�
��b1=c3=3ʱ��d=1����ʱcn=n��ֻ��ȡan=n�����ȱ�����{bn}����ǵȲ�����{an}���е������Sn=$\frac{n��n+1��}{2}$������8�֣�
��b1=c2=3ʱ��d=2����ʱcn=2n-1��ֻ��ȡan=2n-1��
��3n=2m-1����m=$\frac{{3}^{n}+1}{2}$��3n��������3n+1 ����ż����m���������⣬
���Եȱ�����{bn}����ǵȲ�����{an}�е������Sn=n2������10�֣�
��������������{cn}��ǰn���Sn=$\frac{n��n+1��}{2}$����Sn=n2������11�֣�
��3�����ڵȲ�����{an}��ֻ������a1�ʣ�1��q��������d=q-1����13�֣�
��֤bn��bn+1֮������{an}������Ϊbn����֤������������n������$\left\{\begin{array}{l}{{b}_{n}��{a}_{{b}_{1}+{b}_{2}+��+{b}_{n-1}+1}}\\{{b}_{n+1}��{a}_{{b}_{1}+{b}_{2}+��+{b}_{n}}}\end{array}\right.$��
��$\left\{\begin{array}{l}{{b}_{n}��{a}_{1+q+��+{q}^{n-2}+1}}\\{{b}_{n+1}��{a}_{1+q+��+{q}^{n-1}}}\end{array}\right.$������
��bn-${a}_{1+q+��+{q}^{n-2}+1}$=qn-1-a1-��1+q+��+qn-2����q-1��=1-a1��0��
bn+1-${a}_{1+q+��+{q}^{n-1}}$=qn-a1-��1+q+��+qn-1-1����q-1��=q-a1��0����
��������a1�ʣ�1��q��������d=q-1�ĵȲ�����{an}�������⡭��16�֣�
���� ���⿼�������е��ƹ�ϵ���Ȳ�������ȱ����е�ͨ�ʽ���ʽ�������ʡ��������۷�������������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ӡˢ����x��ǧ�ᣩ | 2 | 3 | 4 | 5 | 8 |
| ����ɱ�y��Ԫ�� | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
| ӡˢ����x��ǧ�ᣩ | 2 | 3 | 4 | 5 | 8 | |
| ����ɱ�y��Ԫ�� | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ģ�ͼ� | ����ֵ$\widehat{{y}_{i}}$��1�� | 2.4 | 2.1 | 1.6 | ||
| ��ֵ$\widehat{{e}_{i}}$��1�� | 0 | -0.1 | 0.1 | |||
ģ���� | ����ֵ$\widehat{{y}_{i}}$��2�� | 2.3 | 2 | 1.9 | ||
| ��ֵ$\widehat{{e}_{i}}$��2�� | 0.1 | 0 | 0 | |||
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
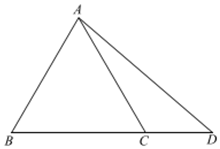 �ڡ�ABC�У���A��B��C�Ա߷ֱ�Ϊa��b��c��a2+b2+c2=ab+bc+ca��
�ڡ�ABC�У���A��B��C�Ա߷ֱ�Ϊa��b��c��a2+b2+c2=ab+bc+ca���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
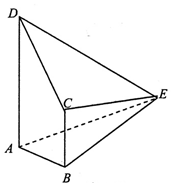 ��ͼ��������E-ABCD�У�ƽ��CDE��ƽ��ABCD����DAB=��ABC=90�㣬AB=BC=1��AD=ED=3��EC=2��
��ͼ��������E-ABCD�У�ƽ��CDE��ƽ��ABCD����DAB=��ABC=90�㣬AB=BC=1��AD=ED=3��EC=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com