
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)通过讨论a的范围,求出函数的导数,得到函数的单调区间,从而确定a的范围即可.
解答 解:(1)当a=1时,f'(x)=$\frac{x(x+3)}{(x+1)^{2}}$,f(x)在定义域 (-1,+∞)
∴f'(x)在(-1,0)上为减函数,在 (0,+∞)上为增函数,
∴函数的减区间为(-1,0),增区间为(0,+∞);
(2)①当a≥1时,由于x∈[0,+∞),
∴$f'(x)=aln({x+1})+\frac{2}{x+1}+ax-2≥ln({x+1})+\frac{2}{x+1}+x-2≥0$,
所以满足f(x)在[0,+∞)上为单调增函数,即a≥1;
②当0<a<1时,f'(x)=aln(x+1)+$\frac{2}{x+1}$+ax-2,
f''(x)=$\frac{a{x}^{2}+3ax+2a-2}{(s+1)^{2}}$,由方程ax2+3ax+2a-2=0的判别式:
△=a2+8a>0,所以方程有两根x1,x2,且由${x_1}{x_2}=\frac{{2({a-1})}}{a}<0$,
∴x1<0<x2,
∴f'(x)在[0,x2]上为减函数,由f'(0)=0可知,在x∈[0,x2]时,f'(x)<0,
这与 f(x)在[0,+∞)上为单调增函数相矛盾.
③当a≤0时,∵$f'(x)=aln({x+1})+\frac{2}{x+1}+ax-2$,
∴f″(x)=$\frac{{ax}^{2}+3ax+2a-2}{{(x+1)}^{2}}$<0,
∴f'(x)在[0,+∞)上为减函数,由f'(0)=0可知,
在x∈(0,+∞)时,f'(x)<0,
这与 f(x)在[0,+∞)上为单调增函数也是相矛盾,
综上所述:实数a的取值范围是[0,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
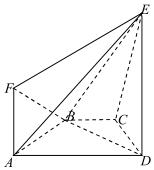 如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.
如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{1}{6},\frac{1}{4}]$ | B. | $[\frac{1}{6},\frac{7}{12}]$ | C. | $[\frac{1}{4},\frac{1}{2}]$ | D. | $[0,\frac{1}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com