
| A. | (-∞,-3] | B. | (-∞,2e] | C. | (-∞,3] | D. | (-∞,2e2+2e] |
分析 令f′(x)≥0在[1,e]上恒成立,对b进行讨论得出b的范围.
解答 解:f′(x)=lnx+$\frac{x-b}{x}$+2x=lnx-$\frac{b}{x}$+1+2x,
∵f(x)在[1,e]上单调递增,∴f′(x)≥0在[1,e]上恒成立,
若b≤0,显然f′(x)>0恒成立,符合题意,
若b>0,则f′′(x)=$\frac{1}{x}$+$\frac{b}{{x}^{2}}$+2>0,
∴f′(x)在[1,e]上是增函数,
∴f′(x)≥f′(1)≥0,即-b+1+2≥0,解得0<b≤3,
综上,b的范围是(-∞,3].
故选:C.
点评 本题考查了函数的单调性与导数的关系,函数的最值计算,属于中档题.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2+\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{3\root{3}{2}}{2}$ | C. | 2 | D. | $\root{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-2,0) | C. | (-1,0) | D. | (-2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
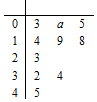 已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
已知函数$f(x)={x^2}+\sqrt{2}(m-1)x+\frac{m}{4}$,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 3 | C. | 8 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com