
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的极值即可;
(Ⅱ)得到$ln{x_1}-{x_1}=\frac{1}{3}mx_2^3-m{x_2}$;设h(x)=lnx-x在(1,2)上的值域为A,函数$g(x)=\frac{1}{3}mx{\;}^3-mx$在(1,2)上的值域为B,根据函数的单调性求出m的范围即可.
解答 解:(Ⅰ)依题意,f(x)=-x-lnx+x2,$f'(x)=-1-\frac{1}{x}+2x=\frac{{2{x^2}-x-1}}{x}=\frac{{({2x+1})({x-1})}}{x}$,
因为x∈(0,+∞),故当x∈(0,1)时,f'(x)<0,当x∈(1,+∞)时,f'(x)>0,
故当x=1时,f(x)有极小值,极小值为f(1)=0,无极大值.
(Ⅱ)当a=1时,f(x)=x-lnx+x2.
因为?x1∈(1,2),?x2∈(1,2),使得$f({x_1})-x_1^2=m{x_2}-\frac{1}{3}mx_2^3({m≠0})$,
故$ln{x_1}-{x_1}=\frac{1}{3}mx_2^3-m{x_2}$;设h(x)=lnx-x在(1,2)上的值域为A,
函数$g(x)=\frac{1}{3}mx{\;}^3-mx$在(1,2)上的值域为B,
当x∈(1,2)时,$h'(x)=\frac{1}{x}-1<0$,即函数h(x)在(1,2)上单调递减,
故h(x)∈(ln2-2,-1),又g'(x)=mx2-m=m(x+1)(x-1).
(i)当m<0时,g(x)在(1,2)上单调递减,此时g(x)的值域为$B=({\frac{2m}{3},-\frac{2m}{3}})$,
因为A⊆B,又$-\frac{2m}{3}>0>-1$,故$\frac{2m}{3}≤ln2-2$,即$m≤\frac{3}{2}ln2-3$;
(ii)当m>0时,g(x)在(1,2)上单调递增,
此时g(x)的值域为$B=({-\frac{2m}{3},\frac{2m}{3}})$,因为A⊆B,又$\frac{2}{3}m>0>-1$,
故$-\frac{2m}{3}≤ln2-2$,故$m≥-\frac{3}{2}({ln2-2})=3-\frac{3}{2}ln2$;
综上所述,实数m的取值范围为$(-∞,\frac{3}{2}ln2-3]∪[3-\frac{3}{2}ln2,+∞)$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3] | B. | (-∞,2e] | C. | (-∞,3] | D. | (-∞,2e2+2e] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
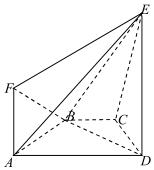 如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.
如图所示,等腰梯形ABCD的底角 A等于60°,直角梯形 ADEF所在的平面垂直于平面ABCD,∠EDA=90°,且ED=AD=2AB=2AF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com