
| A. | [1,e] | B. | [e-1-1,1] | C. | [1,e+1] | D. | [e-1-1,e+1] |
分析 考查题设中的条件,函数f(f(y0))的解析式不易得出,直接求最值有困难,考察四个选项,发现有两个特值区分开了四个选项,0出现在了B,D两个选项的范围中,e+1出现在了C,D两个选项所给的范围中,故可通过验证参数为0与e+1时是否符合题意判断出正确选项.
解答 解:曲线y=cosx上存在点(x0,y0)使得f(f(y0))=y0,则y0∈[-1,1]
考查四个选项,B,D两个选项中参数值都可取0,C,D两个选项中参数都可取e+1,
A,B,C,D四个选项参数都可取1,
由此可先验证参数为0与e+1时是否符合题意,即可得出正确选项
当a=0时,f(x)=$\sqrt{{e}^{x}+2x}$,是一个增函数,且函数值恒非负,
故只研究y0∈[0,1]时f(f(y0))=y0是否成立
由于f(x)=$\sqrt{{e}^{x}+2x}$是一个增函数,可得出f(y0)≥f(0)=1,
而f(1)=$\sqrt{e+2}$>1,故a=0符合题意,由此知A、C两个选项不正确
当a=e+1时,f(x)=$\sqrt{{e}^{x}+2x-e-1}$,此函数是一个增函数,
f(1)=$\sqrt{e+2-e-1}$=1,f(f(1))=f(1)=1,
故a=e+1符合题意,故A,B两个选项不正确
综上讨论知,可确定A、B,C三个选项不正确.
故D选项正确.
故选:D.
点评 本题是一个函数综合题,解题的关键与切入点是观察出四个选项中同与不同点,判断出参数0与e+1是两个特殊值,结合排除法做题的技巧及函数的性质判断出正确选项,本题考查了转化的思想,观察探究的能力,属于考查能力的综合题,易因为找不到入手处致使无法解答失分,易错.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:解答题
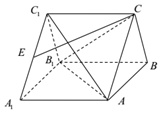 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E为A1C1的中点,$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E为A1C1的中点,$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数大于等于120分 | 分数不足120分 | 合 计 | |
| 周做题时间不少于15小时 | 15 | 4 | 19 |
| 周做题时间不足15小时 | 10 | 16 | 26 |
| 合 计 | 25 | 20 | 45 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com