解:(1)∵f'(x)=-3x
2-4mx-m
2,所以f'(2)=-12-8m-m
2=-5,
解得m=-1或m=-7(舍),即m=-1(3分)
(2)由f'(x)=-3x
2+4x-1=0,解得

,

∴函数f(x)在区间[0,1]的最小值为
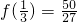
.
(3)∵f(x)=-x
3+2x
2-x+2=(1+x
2)(2-x),
由(2)知,当x∈[0,1]时,
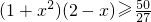
,
∴
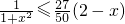
,
∴

.
当a≥0,b≥0,c≥0,且a+b+c=1时,0≤a≤1,0≤b≤1,0≤c≤1,
所以
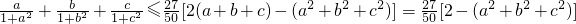
又因为(a+b+c)
2=a
2+b
2+c
2+2ab+2bc+2ca≤3(a
2+b
2+c
2),
所以
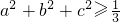
,
故
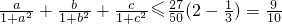
(当且仅当
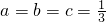
时取等号).
分析:(1)求出函数的导数,f'(x)=-3x
2-4mx-m
2,函数f(x)图象在x=2处的切线与直线y=-5x+12平行,可得函数f(x)=-x
3-2mx
2-m
2x+1-m的图象在x=2处的切线得斜率为-5,也即f′(2)=-5,代入f'(x)=-3x
2-4mx-m
2即可求解m的值.
(2)求出函数的f(x)的导数,令f′(x)=0,求出其极值点和单调区间,导数利用导数求解最值.
(3)根据f(x)=-x
3+2x
2-x+2=(1+x
2)(2-x),由(2)的结论,可得
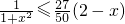
,再根据已知条件,利用不等式间的等价转化求解.
点评:本题主要考查区间上的最值问题,解题的关键是要对函数进行正确的求导,第三问要求掌握不等式间的等价转化,本题难度比较大,是一道难题.

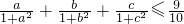 .
. ,
,
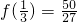 .
.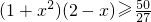 ,
,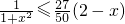 ,
, .
.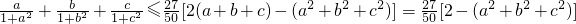
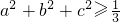 ,
,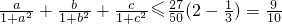 (当且仅当
(当且仅当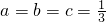 时取等号).
时取等号). ,再根据已知条件,利用不等式间的等价转化求解.
,再根据已知条件,利用不等式间的等价转化求解.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案