
| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
分析 过双曲线左焦点F1(-3,0)且斜率为$\frac{5}{12}$的直线方程为:5x-12y+15=0.
由$\left\{\begin{array}{l}{5x-12y+15=0}\\{5{x}^{2}-4{y}^{2}=20}\end{array}\right.$⇒P(3,$\frac{5}{2}$)所以直线PF2的方程为:x=3,
求出点M到直线PF1,PF2的距离分别为d1、d2,即可
解答 解:过双曲线左焦点F1(-3,0)且斜率为$\frac{5}{12}$的直线方程为:5x-12y+15=0.
由$\left\{\begin{array}{l}{5x-12y+15=0}\\{5{x}^{2}-4{y}^{2}=20}\end{array}\right.$⇒$\left\{\begin{array}{l}{x=3}\\{y=\frac{5}{2}}\end{array}\right.$∴P(3,$\frac{5}{2}$)
所以直线PF2的方程为:x=3,
设点M到直线PF1,PF2的距离分别为d1、d2,
d1=$\frac{5×2-12×1+15}{\sqrt{1{2}^{2}+{5}^{2}}}=1$,d2=1.
则${S_{△PM{F_1}}}-{S_{△PM{F_2}}}$=$\frac{1}{2}(P{F}_{1}-P{F}_{2})×1=a=2$.
故选:C
点评 本题考查了双曲线与直线的位置关系,面积计算,属于中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
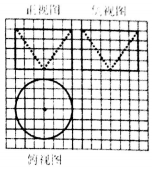 如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )
如图所示,网格纸上小正方形的边长为1,粗线画出的是某一无上盖几何体的三视图,则该几何体的表面积等于( )| A. | 39π | B. | 48π | C. | 57π | D. | 63π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120° | B. | 30° | C. | 90° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com