
分析 (Ⅰ)求出圆的普通方程,然后求解圆C的参数方程;
(Ⅱ)利用圆的参数方程,表示出x+y,通过两角和与差的三角函数,求解最大值,并求出此时点P的直角坐标.
解答 (本小题满分10分)选修4-4:坐标系与参数方程
解:(Ⅰ)因为ρ2=4ρ(cosθ+sinθ)-6,
所以x2+y2=4x+4y-6,
所以x2+y2-4x-4y+6=0,
即(x-2)2+(y-2)2=2为圆C的普通方程.…(4分)
所以所求的圆C的参数方程为$\left\{{\begin{array}{l}{x=2+\sqrt{2}cosθ}\\{y=2+\sqrt{2}sinθ}\end{array}}\right.$(θ为参数).…(6分)
(Ⅱ)由(Ⅰ)可得,$x+y=4+\sqrt{2}(sinθ+cosθ)=4+2sin(θ+\frac{π}{4})$…(7分)
当 $θ=\frac{π}{4}$时,即点P的直角坐标为(3,3)时,…(9分)x+y取到最大值为6.…(10分)
点评 本题考查极坐标与直角坐标,参数方程的应用,考查计算能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
下列命题中错误的是( )
A.如果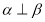 ,那么
,那么 内一定存在直线平行于平面
内一定存在直线平行于平面
B.如果 ,那么
,那么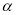 内所有直线都垂直于平面
内所有直线都垂直于平面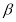
C.如果平面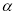 不垂直平面
不垂直平面 ,那么
,那么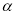 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面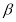
D.如果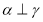 ,
, ,
,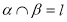 ,那么
,那么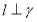
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$({x^2}{)^{\frac{1}{2}}}$,g(x)=$({x^{\frac{1}{2}}}{)^2}$ | B. | f(x)=$\frac{x^2-9}{x+3}$,g(x)=x-3 | ||
| C. | f(x)=${log_2}{x^2}$,g(x)=2log2x | D. | f(x)=x,g(x)=lg10x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>2,x≠4} | B. | [2,4)∪(4,+∞) | C. | {x|x≥2,或x≠4} | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2p}$ | B. | -$\frac{1}{p}$ | C. | $\frac{1}{p}$ | D. | $\frac{1}{2p}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {0,1,3} | D. | B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,则n⊥β | B. | 若m⊥n,n?α,则n⊥β | C. | 若m∥n,则n∥β | D. | 若m∥n,则n⊥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com