
| A. | {x|x>2,x≠4} | B. | [2,4)∪(4,+∞) | C. | {x|x≥2,或x≠4} | D. | [2,+∞) |
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H,设四面体EFGH
的表面积为T,则 等于( )
等于( )
A. 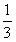 B.
B. 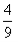 C.
C. 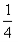 D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
设 ,
,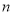 为空间两条不同的直线,
为空间两条不同的直线, ,
,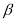 为空间两个不同的平面,给出下列命题:
为空间两个不同的平面,给出下列命题:
①若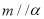 ,
,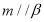 ,则
,则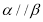 ; ②若
; ②若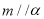 ,
,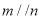 ,则
,则 ;
;
③若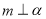 ,
, ,则
,则 ;④若
;④若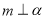 ,
, ,则
,则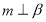 .
.
其中所有正确命题的序号是( )
A.③④ B.②④ C.①② D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{46}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=8x | B. | y2=4x | C. | y2=2x | D. | ${y^2}=4\sqrt{3}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{7}$ | D. | 3$\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com