
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{7}$ | D. | 3$\sqrt{13}$ |
分析 求出双曲线的左焦点得出抛物线的方程,解出A点坐标,取O关于准线的对称点B,则|AB|为|PO|+|PA|的最小值.
解答 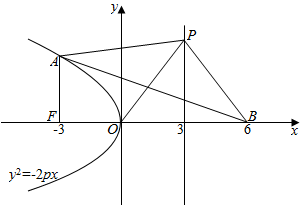 解:双曲线的标准方程为$\frac{{x}^{2}}{8}-{y}^{2}=1$,∴双曲线的左焦点为(-3,0),即F(-3,0).
解:双曲线的标准方程为$\frac{{x}^{2}}{8}-{y}^{2}=1$,∴双曲线的左焦点为(-3,0),即F(-3,0).
∴抛物线的方程为y2=-12x,抛物线的准线方程为x=3,
∵|AF|=6,∴A到准线的距离为6,∴A点横坐标为-3,不妨设A在第二象限,则A(-3,6).
设O关于抛物线的准线的对称点为B(6,0),连结AB,则|PO|=|PB|,
∴|PO|+|PA|的最小值为|AB|.
由勾股定理得|AB|=$\sqrt{A{F}^{2}+B{F}^{2}}$=$\sqrt{117}$=3$\sqrt{13}$.
故选:D.
点评 本题考查了抛物线,双曲线的性质,属于中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x>2,x≠4} | B. | [2,4)∪(4,+∞) | C. | {x|x≥2,或x≠4} | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
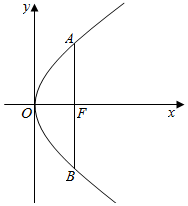 如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.
如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,则n⊥β | B. | 若m⊥n,n?α,则n⊥β | C. | 若m∥n,则n∥β | D. | 若m∥n,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com