
分析 如图所示,设|AT|=m,|FT|=2m,即|AF|=3m.由△AOT∽△OFT,可得:|OT|2=|TF||AT|,解得m.又|OT|=2,可得b2=2+m2.c2=9m2-b2=12.可得a2=b2+c2,即可得出.
解答 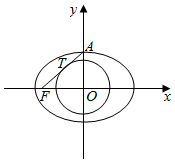 解:如图所示,设|AT|=m,|FT|=2m,即|AF|=3m.
解:如图所示,设|AT|=m,|FT|=2m,即|AF|=3m.
由△AOT∽△OFT,可得:|OT|2=|TF||AT|,
∴4=2m2,解得m=$\sqrt{2}$.
又|OT|=2,∴b2=2+22=6.c2=9m2-b2=12.
∴a2=b2+c2=18.
∴椭圆C的标准方程为$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{6}$=1.
故答案为:$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{6}$=1.
点评 本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、勾股定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
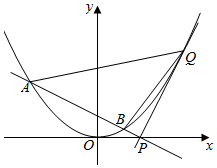 已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.
已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\sqrt{2}$ | C. | m<-1 | D. | $m<-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{7}$ | D. | 3$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.
如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>p>n | B. | p>n>m | C. | n>m>p | D. | m>n>p |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com