练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．如图，某城市有一个五边形的地下污水管通道ABCDE，四边形BCDE是矩形，其中CD=8km，BC=3km；△ABE是以BE为底边的等腰三角形，AB=5km．现欲在BE的中间点P处建地下污水处理中心，为此要过点P建一个“直线型”的地下水通道MN接通主管道，其中接口处M点在矩形BCDE的边BC或CD上．
    （1）若点M在边BC上，设∠BPM=θ，用θ表示BM和NE的长；
    （2）点M设置在哪些地方，能使点M，N平分主通道ABCDE的周长？请说明理由．

    分析 （1）根据条件结合三角形的边角公式建立函数关系即可．
    （2）根据正弦定理结合三角函数的性质进行求解．

    解答 解：（1）当点M在边BC上，设∠BPM=θ$（0≤tanθ≤\frac{3}{4}）$，
    在Rt△BPM中，BM=BP•tanθ=4tanθ．
    在△PEN中，不妨设∠PEN=α，其中$sinα=\frac{3}{5}，cosα=\frac{4}{5}$，则$\frac{PE}{sin（π-θ-α）}=\frac{NE}{sinθ}$，
    即$NE=\frac{4sinθ}{sin（θ+α）}=\frac{20sinθ}{4sinθ+3cosθ}=\frac{20tan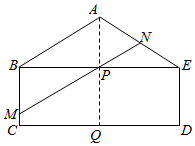θ}{4tanθ+3}$；

    （2）当点M在边BC上，由BM+AB+AN=MC+CD+DE+EN，BM-NE=2；
    即$2tanθ-\frac{10tanθ}{4tanθ+3}=1$；即8tan2θ-8tanθ-3=0，解得$tanθ=\frac{{2±\sqrt{10}}}{4}$．
    ∵$tanθ=\frac{{2-\sqrt{10}}}{4}＜0，tanθ=\frac{{2+\sqrt{10}}}{4}＞\frac{3}{4}$与$0≤tanθ≤\frac{3}{4}$矛盾，点只能设在CD上．
    当点M在边CD上，设CD中点为Q，由轴对称不妨设M在CQ上，此时点N在线段AE上；设∠MPQ=θ$（0≤tanθ≤\frac{4}{3}）$，
    在Rt△MPQ中，MQ=PQ•tanθ=3tanθ；
    在△PAN中，不妨设∠PAE=β，其中$sinβ=\frac{4}{5}，cosβ=\frac{3}{5}$；
    则$\frac{PA}{sin（π-θ-β）}=\frac{AN}{sinθ}$，即$AN=\frac{3sinθ}{sin（θ+β）}=\frac{15sinθ}{3sinθ+4cosθ}=\frac{15tanθ}{3tanθ+4}$；
    由MC+CB+BA+AN=MQ+QD+DE+EN，得AN=MQ，即$3tanθ=\frac{15tanθ}{3tanθ+4}$；解得tanθ=0或$tanθ=\frac{1}{3}$；
    故当CM=4，或者$CM=4-3×\frac{1}{3}=3$时，符合题意．
    答：当点M位于CD中点Q处，或点M到点C的距离为3km时，才能使点M，N平分地下水总通道ABCDE的周长．

    点评 本题主要考查三角函数的应用问题，根据正弦定理建立方程公式以及利用三角函数的公式进行化简是解决本题的关键．综合性较强，有一定的难度．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．已知⊙M的圆心在抛物线x2=4y上，且⊙M与y轴及抛物线的准线都相切，则⊙M的方程是（　　）
    A．x2+y2±4x-2y+1=0B．x2+y2±4x-2y-1=0C．x2+y2±4x-2y+4=0D．x2+y2±4x-2y-4=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知抛物线C：y2=6x，过抛物线的焦点F的直线l交抛物线于点A，交抛物线的准线于点B，若$\overrightarrow{FB}$=3$\overrightarrow{FA}$，则点A到原点的距离为$\frac{\sqrt{13}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知点A、F分别是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的上顶点和左焦点，若AF与圆O：x2+y2=4相切于点T，且点T是线段AF靠近点A的三等分点，则椭圆C的标准方程为$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{6}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在极坐标系中，过点M（2，0）的直线l与极轴的夹角α=$\frac{π}{6}$．
    （1）将l的极坐标方程写成ρ=f（θ）的形式；
    （2）在极坐标系中，以极点为坐标原点，以极轴为x轴的非负半轴建立平面直角坐标系．若曲线C2：$\left\{{\begin{array}{l}{x=3sinθ}\\{y=acosθ}\end{array}}$（θ为参数，a∈R）与直线l有一个公共点在y轴上，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知实数a，b满足|a+b|≤2，求证：|a2+2a-b2+2b |≤4（|a|+2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．棱长为a的正方体ABCD-A1B1C1D1中，若与D1B平行的平面截正方体所得的截面面积为S，则S的取值范围是（0，$\frac{\sqrt{6}}{2}{a}^{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某市于今年1月1日起实施小汽车限购政策．根据规定，每年发放10万个小汽车名额，其中电动小汽车占20%，通过摇号方式发放，其余名额通过摇号和竞价两种方式各发放一半．政策推出后，某网站针对不同年龄段的申请意向进行了调查，结果如下表所示：
    申请意向
    年龄    		摇号竞价（人数）合计
    电动小汽车（人数）非电动小汽车（人数）
    30岁以下
    （含30岁）    		5010050200
    30至50岁
    （含50岁）    		50150300500
    50岁以上10015050300
    合计2004004001000
    （1）采取分层抽样的方式从30至50岁的人中抽取10人，求其中各种意向人数；
    （2）用样本估计总体，在全体市民中任意选取4人，其中摇号申请电动小汽车意向的人数记为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．2位男生和3位女生共5位同学站成一排，则3位女生中有且只有两位女生相邻的排法种数是（　　）
    A．36B．72C．48D．108

    查看答案和解析>>

    同步练习册答案