
分析 (1)先得出直线l的直角坐标方程,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出极坐标方程.
(2)直线l的直角坐标方程为:y=$\frac{\sqrt{3}}{3}$(x-2),令x=0,可得y=-$\frac{2\sqrt{3}}{3}$.曲线C2:$\left\{{\begin{array}{l}{x=3sinθ}\\{y=acosθ}\end{array}}$(θ为参数,a∈R),a≠0时化为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{a}^{2}}$=1,把$(0,-\frac{2\sqrt{3}}{3})$代入上述方程解出即可得出.a=0时,不满足条件,舍去.
解答 解:(1)直线l的直角坐标方程为:y=$\frac{\sqrt{3}}{3}$(x-2),化为极坐标方程:ρcosθ-$\sqrt{3}ρsinθ$-2=0,可得:ρ=$\frac{2}{cosθ-\sqrt{3}sinθ}$=$\frac{-1}{sin(θ-\frac{π}{6})}$.
(2)直线l的直角坐标方程为:y=$\frac{\sqrt{3}}{3}$(x-2),令x=0,可得y=-$\frac{2\sqrt{3}}{3}$.
曲线C2:$\left\{{\begin{array}{l}{x=3sinθ}\\{y=acosθ}\end{array}}$(θ为参数,a∈R),a≠0时化为:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{a}^{2}}$=1,
把$(0,-\frac{2\sqrt{3}}{3})$代入上述方程可得:a=$±\frac{2\sqrt{3}}{3}$.
a=0时,不满足条件,舍去.
综上可得:a=$±\frac{2\sqrt{3}}{3}$.
点评 本题考查了极坐标方程与直角坐标方程的互化、椭圆的参数方程、直线与曲线的交点,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [1+$\frac{π}{6}$,2+$\frac{π}{6}$) | B. | [1+$\frac{π}{3}$,2+$\frac{π}{3}$) | C. | [$\frac{1}{2}$+$\frac{π}{6}$,1+$\frac{π}{6}$) | D. | [$\frac{1}{2}$+$\frac{π}{3}$,1+$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.
如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
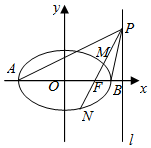 已知A,B是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点,F为其右焦点,在直线x=4上任取一点P(点P不在x轴上),连结PA,PF,PB.若半焦距c=1,且2kPF=kPA+kPB
已知A,B是椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左,右顶点,F为其右焦点,在直线x=4上任取一点P(点P不在x轴上),连结PA,PF,PB.若半焦距c=1,且2kPF=kPA+kPB查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,且椭圆过点(0,$\sqrt{3}}$),(${\sqrt{3}$,-$\frac{{\sqrt{6}}}{2}}$),且A是椭圆上位于第一象限的点,且△AF1F2的面积S${\;}_{△A{F_1}{F_2}}}$=$\sqrt{3}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,且椭圆过点(0,$\sqrt{3}}$),(${\sqrt{3}$,-$\frac{{\sqrt{6}}}{2}}$),且A是椭圆上位于第一象限的点,且△AF1F2的面积S${\;}_{△A{F_1}{F_2}}}$=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,5] | B. | [-2,5] | C. | [1,7] | D. | [-2,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com