
分析 根据等等边三角形的性质求出A点坐标,代入抛物线方程计算p.
解答 解:由抛物线的对称性可知A,B关于y轴对称,不妨设A(a,b)在第一象限.
∵△ABO为等边三角形,∴∠AOM=30°.
∵|MA|=|MO|=10,∴∠OMA=120°.
∴|OA|=$\sqrt{|O{M|}^{2}+|MA{|}^{2}-2|OM|•|MA|cos120°}$=10$\sqrt{3}$.
∴A(5$\sqrt{3}$,15).
∴(5$\sqrt{3}$)2=2p×15,解得p=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了抛物线的性质,解三角形,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
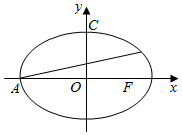 已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1,点A,C分别为椭圆C的左顶点和上顶点,点F为椭圆的右焦点,设过点A的直线交椭圆C与另一点M.
已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1,点A,C分别为椭圆C的左顶点和上顶点,点F为椭圆的右焦点,设过点A的直线交椭圆C与另一点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com