
分析 (1)将a=0代入f(x),求出f(x)的导数,得到f′(x)=3,解得x的值,求出切点坐标,代入求出m的值即可;
(2)假设函数f(x)在[1,3]上不存在单调递增区间,必有g(x)≤0,得到关于a的不等式组,解出即可.
解答 解:(1)当a=0时,f(x)=lnx+x2,x∈(0,+∞),
f′(x)=$\frac{1}{x}$+2x>0,
令f′(x)=3,解得:x=1或x=$\frac{1}{2}$,
代入f(x)得切点坐标为(1,1),或($\frac{1}{2}$,$\frac{1}{4}$-ln2),
将切点坐标代入直线y=3x+m,解得:m=-2或m=-$\frac{5}{4}$-ln2;
(2)f′(x)=$\frac{1}{x}$+2x-2a=$\frac{{2x}^{2}-2ax+1}{x}$,x∈[1,3],
设g(x)=2x2-2ax+1,
假设函数f(x)在[1,3]上不存在单调递增区间,必有g(x)≤0,
于是$\left\{\begin{array}{l}{g(1)=3-2a≤0}\\{g(3)=19-6a≤0}\end{array}\right.$,解得:a≥$\frac{19}{6}$,
故要使函数f(x)在[1,3]上存在单调递增区间,
则a的范围是(-∞,$\frac{19}{6}$).
点评 本题考查了函数的单调性问题,考查曲线的切线方程以及导数的应用,是一道中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:解答题
某中学举行了一次“环保知识竞赛”活动. 为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为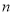 )进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
)进行统计. 按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).
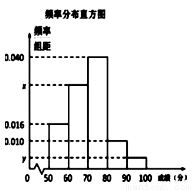
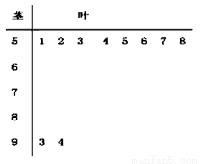
(1)求样本容量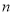 和频率分布直方图中的
和频率分布直方图中的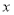 ,
, 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设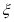 表示所抽取的3名同学中得分在[80,90)的学生人数,求
表示所抽取的3名同学中得分在[80,90)的学生人数,求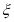 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1+$\frac{π}{6}$,2+$\frac{π}{6}$) | B. | [1+$\frac{π}{3}$,2+$\frac{π}{3}$) | C. | [$\frac{1}{2}$+$\frac{π}{6}$,1+$\frac{π}{6}$) | D. | [$\frac{1}{2}$+$\frac{π}{3}$,1+$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.
如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
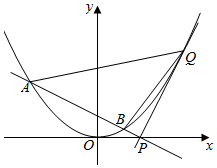 已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.
已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,且椭圆过点(0,$\sqrt{3}}$),(${\sqrt{3}$,-$\frac{{\sqrt{6}}}{2}}$),且A是椭圆上位于第一象限的点,且△AF1F2的面积S${\;}_{△A{F_1}{F_2}}}$=$\sqrt{3}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,且椭圆过点(0,$\sqrt{3}}$),(${\sqrt{3}$,-$\frac{{\sqrt{6}}}{2}}$),且A是椭圆上位于第一象限的点,且△AF1F2的面积S${\;}_{△A{F_1}{F_2}}}$=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com