
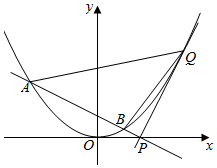
 已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.
已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.分析 (I)设直线l1斜率为k,得出l1的方程,联立方程组,根据方程只有一解得出k与t的关系,从而得出l2的斜率,得出l2的点斜式方程化简即可;
(II)联立l2与抛物线的方程,得出根与系数的关系,代入斜率公式化简$k_1^2+k_2^2$,利用基本不等式求出最小值成立的条件,从而得出t.
解答 解:(Ⅰ)设直线l1的斜率为k,则直线l1的方程为y=k(x-t),
联立方程组$\left\{\begin{array}{l}{x^2}=4y\\ y=k(x-t)\end{array}\right.$,消元得:x2-4kx+4kt=0,
∵直线l1与抛物线C相切,
∴△=16k2-16kt=0,解得t=k,∴Q(2t,t2),
∵l1⊥l2,∴直线l2的斜率为-$\frac{1}{t}$,则直线l2的方程为:$y=-\frac{1}{t}(x-t)$,即$y=-\frac{1}{t}x+1$,
∴直线l2恒过定点(0,1);
(Ⅱ)设$A({x_1},\frac{x_1^2}{4})$,$B({x_2},\frac{x_2^2}{4})$,
联立方程组$\left\{\begin{array}{l}{x^2}=4y\\ y=-\frac{1}{t}x+1\end{array}\right.$,消元得:${x^2}+\frac{4}{t}x-4=0$,
∴${x_1}+{x_2}=-\frac{4}{t}$,x1x2=-4,
∴${k_1}=\frac{{{t^2}-\frac{x_1^2}{4}}}{{2t-{x_1}}}=\frac{1}{4}(2t+{x_1})$,同理得出:${k_2}=\frac{1}{4}(2t+{x_2})$,
∴$k_1^2+k_2^2=\frac{1}{16}[{(2t+{x_1})^2}+{(2t+{x_2})^2}]$=$\frac{1}{16}$(8t2+x12+x22+4tx1+4tx2)
=$\frac{1}{16}[{({x_1}+{x_2})^2}+4t({x_1}+{x_2})-2{x_1}{x_2}+8{t^2}]$
=$\frac{1}{16}[\frac{16}{t^2}-16+8+8{t^2}]$
=$\frac{1}{2}[\frac{2}{t^2}+{t^2}-1]≥\sqrt{2}-\frac{1}{2}$.
当且仅当$\frac{2}{{t}^{2}}={t}^{2}$即$t=\root{4}{2}$时,取得等号.
$k_1^2+k_2^2$取得最小值时,P的坐标为$P(\root{4}{2},0)$.
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | x2+y2±4x-2y+1=0 | B. | x2+y2±4x-2y-1=0 | C. | x2+y2±4x-2y+4=0 | D. | x2+y2±4x-2y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 申请意向 年龄 | 摇号 | 竞价(人数) | 合计 | |
| 电动小汽车(人数) | 非电动小汽车(人数) | |||
| 30岁以下 (含30岁) | 50 | 100 | 50 | 200 |
| 30至50岁 (含50岁) | 50 | 150 | 300 | 500 |
| 50岁以上 | 100 | 150 | 50 | 300 |
| 合计 | 200 | 400 | 400 | 1000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com