
| 申请意向 年龄 | 摇号 | 竞价(人数) | 合计 | |
| 电动小汽车(人数) | 非电动小汽车(人数) | |||
| 30岁以下 (含30岁) | 50 | 100 | 50 | 200 |
| 30至50岁 (含50岁) | 50 | 150 | 300 | 500 |
| 50岁以上 | 100 | 150 | 50 | 300 |
| 合计 | 200 | 400 | 400 | 1000 |
分析 (1)采取分层抽样的方式从30至50岁的人中抽取10人,每个人被抽到的概率为$\frac{1}{50}$,由此能求出各种意向人数.
(2)根据题意得出X~B(4,$\frac{1}{5}$),由此能求出X的分布列和E(X).
解答 解:(1)采取分层抽样的方式从30至50岁的人中抽取10人,
∵30至50岁的有500人,
∴每个人被抽到的概率为p1=$\frac{10}{500}$=$\frac{1}{50}$,
根据题意得出:电动小汽车,摇号的有50×$\frac{1}{50}$=1,
非电动小汽车,摇号的有300×$\frac{1}{50}$=6.
(2)根据题意得出:样本总人数1000人,电动小汽车摇号的有200人,
非电动小汽车摇号的有400人,竞价的有400人,总共有1000人,
用样本估计总体,在全体市民中任意选取4人,其中摇号申请电动小汽车意向的概率为p=$\frac{200}{100}=\frac{1}{5}$,
摇号申请电动小汽车意向的人数记为X,X=0,1,2,3,4,且X~B(4,$\frac{1}{5}$),P(X=0)=${C}_{4}^{0}(\frac{4}{5})^{4}$=$\frac{256}{625}$,
P(X=1)=${C}_{4}^{1}(\frac{1}{5})(\frac{4}{5})^{3}$=$\frac{256}{625}$,
P(X=2)=${C}_{4}^{2}(\frac{1}{5})^{2}(\frac{4}{5})^{2}$=$\frac{96}{625}$,
P(X=3)=${C}_{4}^{3}(\frac{1}{5})^{3}(\frac{4}{5})$=$\frac{16}{625}$,
P(X=4)=${C}_{4}^{4}(\frac{1}{5})^{4}=\frac{1}{625}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{256}{625}$ | $\frac{256}{625}$ | $\frac{96}{625}$ | $\frac{16}{625}$ | $\frac{1}{625}$ |
点评 本题考查分层抽样的应用,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:解答题
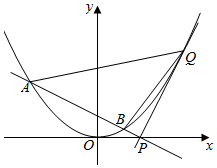 已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.
已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.
如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>p>n | B. | p>n>m | C. | n>m>p | D. | m>n>p |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,且椭圆过点(0,$\sqrt{3}}$),(${\sqrt{3}$,-$\frac{{\sqrt{6}}}{2}}$),且A是椭圆上位于第一象限的点,且△AF1F2的面积S${\;}_{△A{F_1}{F_2}}}$=$\sqrt{3}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,且椭圆过点(0,$\sqrt{3}}$),(${\sqrt{3}$,-$\frac{{\sqrt{6}}}{2}}$),且A是椭圆上位于第一象限的点,且△AF1F2的面积S${\;}_{△A{F_1}{F_2}}}$=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{3}$=1(x>1) | B. | x2-$\frac{{y}^{2}}{5}$=1(x<-1) | C. | x2-$\frac{{y}^{2}}{3}$=1(x<0) | D. | x2-$\frac{{y}^{2}}{3}$=1(x<-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com