Question

18．已知点M（-2，0），N（2，0），B（-1，0），动圆C与直线MN相切于点B，过M，N与圆C相切的两直线相交于点P（异于点M，N），则P点的轨迹方程为（　　）

• A． x²-$\frac{{y}^{2}}{3}$=1（x＞1）
• B． x²-$\frac{{y}^{2}}{5}$=1（x＜-1）
• C． x²-$\frac{{y}^{2}}{3}$=1（x＜0）
• D． x²-$\frac{{y}^{2}}{3}$=1（x＜-1）

Answer 1

分析 PM，PN分别与圆C相切于R、Q，根据圆的切线长定理，能够推导出PN-PM=QN-RM=NB-MB=2＜MN，因此点P的轨迹是以M、N为焦点的双曲线．再根据题条件能够求出P点的轨迹方程

解答 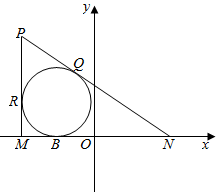解：设PM，PN分别与圆C相切于R、Q．
则PR=PQ，MR=MB，NQ=NB．
∴PN-PM=QN-RM=NB-MB=2＜MN，
∴P点轨迹为以M，N为焦点的双曲线的左支．
设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$，则2a=PN-PM=2，∴a=1．
∵c=2，∴b²=c²-a²=3．
∴双曲线方程为x²-$\frac{{y}^{2}}{3}$=1．（x＜-1）．
故选：D．

点评 本题考查双曲线的基本性质和圆的切线长定理，解题时要注意审题．