
分析 先表述出函数f(x)的解析式然后代入将函数g(x)表述出来,然后对底数a进行讨论即可得到答案
解答 解:已知函数y=f(x)的图象与函数y=ax(a>0且a≠1)的图象关于直线y=x对称,
则f(x)=logax,记g(x)=f(x)[f(x)+f(2)-1]=(logax)2+(loga2-1)logax.
当a>1时,
若y=g(x)在区间[$\frac{1}{2}$,2]上是增函数,y=logax为增函数,
令t=logax,t∈[$lo{g}_{a}\frac{1}{2}$,loga2],要求对称轴-$\frac{lo{g}_{a}^{2}-1}{2}$$≤lo{g}_{a}^{\frac{1}{2}}$,矛盾;
当0<a<1时,若y=g(x)在区间[$\frac{1}{2}$,2]上是增函数,y=logax为减函数,
令t=logax,t∈[loga2,log${\;}_{a}^{\frac{1}{2}}$],要求对称轴$-\frac{lo{g}_{a}^{2}}{2}≥lo{g}_{a}^{\frac{1}{2}}$,
解得a≤$\frac{1}{2}$,
所以实数a的取值范围是(0,$\frac{1}{2}$],
故答案为(0,$\frac{1}{2}$].
点评 本题主要考查指数函数与对数函数互为反函数.这里注意指数函数和对数函数的增减性与底数的大小有关,即当底数大于1时单调递增,当底数大于0小于1时单调递减


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 申请意向 年龄 | 摇号 | 竞价(人数) | 合计 | |
| 电动小汽车(人数) | 非电动小汽车(人数) | |||
| 30岁以下 (含30岁) | 50 | 100 | 50 | 200 |
| 30至50岁 (含50岁) | 50 | 150 | 300 | 500 |
| 50岁以上 | 100 | 150 | 50 | 300 |
| 合计 | 200 | 400 | 400 | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
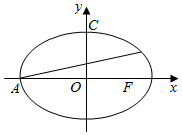 已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1,点A,C分别为椭圆C的左顶点和上顶点,点F为椭圆的右焦点,设过点A的直线交椭圆C与另一点M.
已知椭圆C:$\frac{x^2}{4}$+$\frac{y^2}{3}$=1,点A,C分别为椭圆C的左顶点和上顶点,点F为椭圆的右焦点,设过点A的直线交椭圆C与另一点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com