
分析 由抛物线方程求得焦点坐标,求得|DF|的长度,利用抛物线性质可求得|AF|=|AC|,$\overrightarrow{FB}$=3$\overrightarrow{FA}$可知|AB|=2|AF|=2|AC|,根据三角形可求得|BD|=3$\sqrt{3}$,利用相似三角形可求得|CA|、|CD|的值,即可求得A点坐标,利用两点间的距离公式求得A到原点的距离.
解答 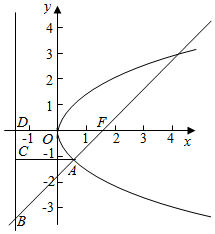 解:抛物线C:y2=6x,准线垂直于x轴,垂足为D,|DF|=3,
解:抛物线C:y2=6x,准线垂直于x轴,垂足为D,|DF|=3,
由抛物线定义,A点到F点的距离等于A到准线的距离,即|AF|=|AC|,
$\overrightarrow{FB}$=3$\overrightarrow{FA}$,即|FB|=3|FA|,|AB|=2|AF|=2|AC|.
∴∠ABC=$\frac{π}{6}$,tan∠ABC=$\frac{丨DF丨}{丨BD丨}$,
∴|BD|=3$\sqrt{3}$,
由相似三角可知,|CA|=$\frac{2}{3}$|DF|=2,|CD|=$\frac{1}{3}$|BD|=$\sqrt{3}$,
A点横坐标为|AC|-$\frac{3}{2}$=$\frac{1}{2}$,
故A点的坐标为($\frac{1}{2}$,-$\sqrt{3}$),
∴点A到原点的距离为$\sqrt{\frac{1}{4}+3}$=$\frac{\sqrt{13}}{2}$,
故答案为:$\frac{\sqrt{13}}{2}$.
点评 本题考查直线与圆锥曲线的位置关系及抛物线的性质,考查学生计算能力及对问题的转化能力,属中档题,


科目:高中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.
如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
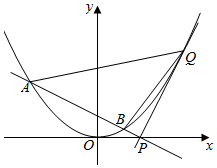 已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.
已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\sqrt{2}$ | C. | m<-1 | D. | $m<-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.
如图,某城市有一个五边形的地下污水管通道ABCDE,四边形BCDE是矩形,其中CD=8km,BC=3km;△ABE是以BE为底边的等腰三角形,AB=5km.现欲在BE的中间点P处建地下污水处理中心,为此要过点P建一个“直线型”的地下水通道MN接通主管道,其中接口处M点在矩形BCDE的边BC或CD上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com