
 如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.
如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.分析 (1)设点M(x0,y0),P(m,-2).得出直线OP的方程,于是M到直线OP的距离等于M到y轴的距离,结合A,M,P三点共线列出方程组解出p,得出抛物线方程;
(2)设Q(a,$\frac{{a}^{2}}{2}$),求出l0的方程,得到A到l0的距离d关于a的函数,利用基本不等式得出函数取得最小值时a的值,从而得出l0方程.
解答 解:(1)设点M(x0,y0),P(m,-2).则直线OP的方程为:2x+my=0.
∵A,M,P三点共线,∴$\frac{{y}_{0}+2}{{x}_{0}-m}=\frac{4}{-m}$,即m=$\frac{4{x}_{0}}{2-{y}_{0}}$.
∵直线OM平分∠POA,
∴M到直线OP的距离等于M到y轴的距离.即$\frac{|2{x}_{0}+m{y}_{0}|}{\sqrt{{m}^{2}+4}}$=|x0|.
∴4x02+4mx0y0+m2y02=4x02+mx02,即m=$\frac{4{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-{{y}_{0}}^{2}}$=$\frac{4{x}_{0}{y}_{0}}{2p{y}_{0}-{{y}_{0}}^{2}}$=$\frac{4{x}_{0}}{2p-{y}_{0}}$.
∴$\frac{4{x}_{0}}{2-{y}_{0}}$=$\frac{4{x}_{0}}{2p-{y}_{0}}$,∴p=1.
∴抛物线C的方程为:x2=2y.
(2)∵x2=2y,∴y=$\frac{{x}^{2}}{2}$,∴y′=x.
设Q(a,$\frac{{a}^{2}}{2}$),则直线l0的方程为;y-$\frac{{a}^{2}}{2}$=a(x-a),即ax-y-$\frac{{a}^{2}}{2}$=0.
∴A到直线l0的距离为d=$\frac{|2+\frac{{a}^{2}}{2}|}{\sqrt{{a}^{2}+1}}$=$\frac{{a}^{2}+4}{2\sqrt{{a}^{2}+1}}$=$\frac{1}{2}$($\sqrt{{a}^{2}+1}$+$\frac{3}{\sqrt{{a}^{2}+1}}$)≥$\sqrt{3}$.
当且仅当$\sqrt{{a}^{2}+1}=\frac{3}{\sqrt{{a}^{2}+1}}$即a=$±\sqrt{2}$时取到等号.
∴当点A到直线l0的距离最小时,直线l0的方程为$\sqrt{2}$x-y-1=0或-$\sqrt{2}$x-y-1=0.
点评 本题考查了抛物线的性质,切线方程,距离公式的应用,属于中档题.


科目:高中数学 来源:2015-2016学年江苏泰兴中学高一下学期期中数学试卷(解析版) 题型:填空题
已知 ,且
,且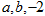 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则
这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则 ____.
____.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2±4x-2y+1=0 | B. | x2+y2±4x-2y-1=0 | C. | x2+y2±4x-2y+4=0 | D. | x2+y2±4x-2y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com