
分析 (Ⅰ)设A(x1,$\frac{1}{2}$x12),B(x2,$\frac{1}{2}$x22),求得函数的导数,可得切线的斜率,进而得到切线的方程,代入(0,-1),求得切点坐标,进而得到|AB|;
(Ⅱ)设P(x,y),由切线的方程求得P的坐标,设直线AB的方程为y=kx+b,代入抛物线的方程,运用韦达定理,可得P的坐标,再由P在直线y=x-1,由直线恒过定点的方法,即可得到定点(1,1).
解答 解:(Ⅰ)设A(x1,$\frac{1}{2}$x12),B(x2,$\frac{1}{2}$x22),
y=$\frac{1}{2}$x2的导数为y′=x,
以A为切点的切线方程为y-$\frac{1}{2}$x12=x1(x-x1),
整理得y=x1x-$\frac{1}{2}$x12,
同理,以B为切点的切线方程为y=x2x-$\frac{1}{2}$x22,
代入P(0,-1),得x12=x22=2(x1x2<0),
可得|AB|=|x1-x2|=2$\sqrt{2}$;
(Ⅱ)证明:设P(x,y),由(Ⅰ)得
$\left\{\begin{array}{l}{y={x}_{1}x-\frac{1}{2}{{x}_{1}}^{2}}\\{y={x}_{2}x-\frac{1}{2}{{x}_{2}}^{2}}\end{array}\right.$可得P($\frac{{x}_{2}+{x}_{1}}{2}$,$\frac{{x}_{1}{x}_{2}}{2}$),
由已知直线AB的斜率必存在,设直线AB的方程为y=kx+b,
$\left\{\begin{array}{l}{y=kx+b}\\{y=\frac{1}{2}{x}^{2}}\end{array}\right.$,可得x2-2kx-2b=0,
即有x1+x2=2k,x1x2=-2b,可得P(k,-b),
由P在直线y=x-1上,可得b=1-k,
则直线AB的方程为y=kx+(1-k),即k(x-1)-y+1=0,
则直线AB过定点(1,1).
点评 本题考查抛物线的方程的运用,注意联立直线方程运用韦达定理,同时考查切线方程的求法,注意运用导数的几何意义,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.
如图所示,在平面直角坐标系xOy中,已知过点A(0,2)的直线与抛物线C:x2=2py(p>0)相交于两点M,N,与直线y=-2相交于点P(M位于A,P之间),直线OM平分∠POA.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=8x | B. | y2=4x | C. | y2=2x | D. | ${y^2}=4\sqrt{3}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
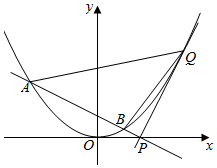 已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.
已知抛物线C:x2=4y,过点P(t,0)(其中t>0)作互相垂直的两直线l1,l2,直线l1与抛物线C相切于点Q(Q在第一象限内),直线l2与抛物线C相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\sqrt{2}$ | C. | m<-1 | D. | $m<-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>p>n | B. | p>n>m | C. | n>m>p | D. | m>n>p |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com