
分析 (Ⅰ)由题意可知,设P(x,y),利用中点坐标公式求得Q(2x,0),R(0,2y),分别求得$\overline{TQ}$和$\overline{QR}$,由$\overrightarrow{TQ}•\overrightarrow{QR}=0$,整理即可求得P的轨迹方程;
(Ⅱ)由(I)可知点E的坐标为(2,2),设出A、B的坐标及直线方程,与抛物线方程联立,整理得到关于x的一元二次方程,根据韦达定理求得x1x2,x1+x2,求得直线AE的方程,分别表示出向量$\overline{OM}$和$\overline{ON}$,并求得$\overline{OM}$•$\overline{ON}$=0,即可求得OM⊥ON,以此$∠MON=\frac{π}{2}$.
解答 解:(Ⅰ)设P(x,y),Q(x0,0),R(0,y0),
∵点P为RQ的中点,
∴$\left\{\begin{array}{l}x=\frac{x_0}{2}\\ y=\frac{y_0}{2}\end{array}\right.$,得$\left\{\begin{array}{l}{x_0}=2x\\{y_0}=2y\end{array}\right.$,
∴Q(2x,0),R(0,2y).(2分)
∵T(0,-4),$\overrightarrow{TQ}•\overrightarrow{QR}=0$,$\overrightarrow{TQ}=(2x,4),\overrightarrow{RQ}=(2x,-2y)$;
∴4x2-8y=0即x2=2y(5分)
(Ⅱ)证明:由(I)可知点E的坐标为(2,2),设$A({x_1},\frac{x_1^2}{2})$,$B({x_2},\frac{x_2^2}{2})$,M(xM,-2),N(xN,-2),
∵直线l与曲线C交于不同的两点A,B(不同于点E).
∴直线l一定有斜率,设直线l方程为y=kx+2(k≠0)(6分)
与抛物线方程联立得到$\left\{\begin{array}{l}y=kx+2\\{x^2}=2y\end{array}\right.$,消去y,得:x2-2kx-4=0
则由韦达定理得:x1x2=-4,x1+x2=2k(7分)
直线AE的方程为:$y-2=\frac{{\frac{x_1^2}{2}-2}}{{{x_1}-2}}({x-2})$,即$y=\frac{{{x_1}+2}}{2}({x-2})+2$,
令y=-2,得${x_M}=\frac{{2{x_1}-4}}{{{x_1}+2}}$同理可得:${x_N}=\frac{{2{x_2}-4}}{{{x_2}+2}}$(9分)
又$\overrightarrow{OM}=({x_M},-2),\overrightarrow{ON}=({x_N},-2)$,
得:$\overrightarrow{OM}•\overrightarrow{ON}={x_M}{x_N}+4=4+\frac{{2{x_1}-4}}{{{x_1}+2}}•\frac{{2{x_2}-4}}{{{x_2}+2}}$,
=$4+\frac{{4[{x_1}{x_2}-2({x_1}+{x_2})+4]}}{{{x_1}{x_2}+2({x_1}+{x_2})+4}}$,
=$4+\frac{4(-4-4k+4)}{(-4+4k+4)}=0$.(11分)
∴OM⊥ON,即∠MON=$\frac{π}{2}$(12分)
点评 本题考查了抛物线的标准方程及其性质、数量积运算性质、直线与抛物线相交转化为方程联立可得根与系数的关系,考查了推理能力与计算能力,属于难题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
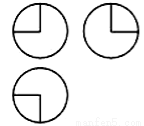
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是 ,则它的表面积是( )
,则它的表面积是( )
A.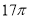 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com