
| A. | $\frac{9}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
分析 利用抛物线的性质得出P点坐标(4,4),根据点共线得出Q点坐标,从而得出|QF|.
解答 解:抛物线的准线方程为:x=-1,交点F(1,0).
设P($\frac{{a}^{2}}{4}$,a),∵|PF|=5,∴$\frac{{a}^{2}}{4}$+1=5,解得a=4,即P(4,4).
设Q($\frac{{b}^{2}}{4}$,b),∵P,F,Q三点共线,∴kPF=kQF.
即$\frac{4}{3}=\frac{b}{\frac{{b}^{2}}{4}-1}$,解得b=-1.即Q($\frac{1}{4}$,-1).
∴|QF|=$\frac{1}{4}+1$=$\frac{5}{4}$.
故选:B.
点评 本题考查了抛物线的简单性质,属于中档题.


科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
定义在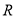 上的奇函数
上的奇函数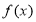 和偶函数
和偶函数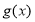 满足:
满足: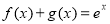 ,给出如下结论:
,给出如下结论:
① 且
且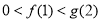 ;
;
②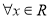 ,总有
,总有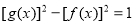 ;
;
③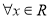 ,总有
,总有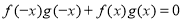 ;
;
④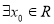 ,使得
,使得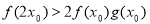 .
.
其中所有正确结论的序号是( )
A.①②③ B.②③ C.①③④ D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{3}$ | B. | -$\frac{1}{3}$ | C. | -$\frac{3}{4}$ | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\sqrt{3}π$ | D. | 3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角 | B. | 直角 | C. | 钝角 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$或$\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com