
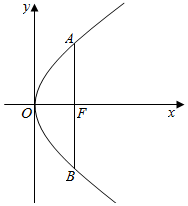
 如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.
如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.分析 (1)求出A,B坐标,利用导数解出切线方程,求出切线与x轴的交点,利用三角形的面积列方程解出p;
(2)计算kOA•kOB=-4,设出MN方程,求出MN与x轴的交点,联立方程组,根据根与系数的关系计算|yM-yN|,得出△OMN面积S关于t的函数,解出函数的最值.
解答 解:(1)抛物线的焦点坐标为F($\frac{p}{2}$,0),∴$A(\frac{p}{2},p),B(\frac{p}{2},-p)$,
由$y=\sqrt{2px}$,得$y'=\frac{p}{{\sqrt{2px}}}$,∴抛物线C在A处的切线斜率为1,
由抛物线C的对称性,知抛物线C在B处的切线卸斜率为-1,
∴抛物线过A点的切线方程为y-p=x-$\frac{p}{2}$,令y=0得x=-$\frac{p}{2}$.
∴$\frac{1}{2}•2p•p=4$,解得p=2.
∴抛物线C的方程为y2=4x.
(2)kOA=2,kOB=-2,∴kOA•kOB=-4,
设$M(\frac{1}{4}y_1^2,{y_1}),N(\frac{1}{4}y_2^2,{y_2})$,则${k_{OM}}•{k_{ON}}=\frac{{{y_1}{y_2}}}{{\frac{1}{16}y_1^2•y_2^2}}=-4$,
∴y1y2=-4.
令直线MN的方程为x=ty+n,
联立方程组$\left\{{\begin{array}{l}{{y^2}=4x}\\{x=ty+n}\end{array}}\right.$消去x得:y2-4ty-4n=0,
则y1y2=-4n,y1+y2=4t,
∵y1y2=-4,∴n=1.即直线MN过点(1,0).
∴${S_{△OMN}}=\frac{1}{2}|{{y_1}-{y_2}}|=\frac{1}{2}\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\frac{1}{2}\sqrt{16{t^2}+16}=2\sqrt{{t^2}+1}$.
∵t2≥0,∴S△OMN≥2.
综上所示,△OMN面积的取值范围是[2,+∞).
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{46}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=8x | B. | y2=4x | C. | y2=2x | D. | ${y^2}=4\sqrt{3}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>1 | B. | $m>\sqrt{2}$ | C. | m<-1 | D. | $m<-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{5}$ | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{7}$ | D. | 3$\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com