
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | D. | (-2,0)∪(0,2) |
分析 可判断f(x)是(-∞,0)∪(0,+∞)上的偶函数,再由函数的单调性解不等式.
解答 解:当x>0时,f(-x)=-ln(-(-x))-x=-lnx-x=f(x),
故f(x)是(-∞,0)∪(0,+∞)上的偶函数;
当x>0时,f(x)=-lnx-x为减函数,
而ln$\frac{1}{2}-2$=-ln2-2=f(2),
故f($\frac{1}{m}$)<ln$\frac{1}{2}-2$=f(2),
故$\frac{1}{m}$>2,
故0<m<$\frac{1}{2}$;
由f(x)是(-∞,0)∪(0,+∞)上的偶函数知,
-$\frac{1}{2}$<m<0;
综上所述,m∈(-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$),
故选C.
点评 本题考查了分段函数的性质的判断与应用,同时考查了分类讨论的思想方法应用.


科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {0,1,3} | D. | B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
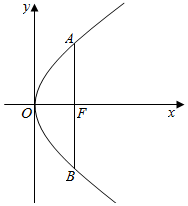 如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.
如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,则n⊥β | B. | 若m⊥n,n?α,则n⊥β | C. | 若m∥n,则n∥β | D. | 若m∥n,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,lg6] | B. | (-∞,3lg2] | C. | [lg6,+∞) | D. | [3lg2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com