
分析 利用正弦定理、三角函数加法定理、倍角公式等知识求解.
解答 解:在△ABC中:
①∵$\frac{sinA}{a}$=$\frac{sinB}{b}$,
∴当A<B时,根据三角形内,大角对大边,得a<b,
∴sinA<sinB,故①正确;
②∵$\frac{a}{sinA}$=$\frac{b}{sinB}$,
当sinA<sinB时,则a<b,根据三角形内,大边对大角,
∴A<B,故②正确;
③则$\frac{1}{tan2A}$-$\frac{1}{tan2B}$=$\frac{cos2A}{sin2A}$-$\frac{cos2B}{sin2B}$=$\frac{cos2Asin2B-cos2Bsin2A}{sin2Asin2B}$=$\frac{sin2(B-A)}{sin2Asin2B}$,
∵A>B,
∴0<A-B<π,
∴sin(B-A)=-sin(A-B)<0,
当0<A≤$\frac{π}{2}$,0<B≤$\frac{π}{2}$时,0<2A≤π,0<2B≤π,0≤A-B≤$\frac{π}{2}$,
sin2A>0,sin2B>0,cos(B-A)>0
∴则$\frac{1}{tan2A}$-$\frac{1}{tan2B}$<0,∴$\frac{1}{tan2A}$<$\frac{1}{tan2B}$;
当$\frac{π}{2}$<A<π,0<B≤$\frac{π}{2}$时(A和B不可能同时在第二象限),π<2A<2π,0<2B≤π,
∴sin2A<0,sin2B>0
当0≤A-B≤时,cos(B-A)>0,
∴则$\frac{1}{tan2A}$-$\frac{1}{tan2B}$>0,∴$\frac{1}{tan2A}$>$\frac{1}{tan2B}$,
当$\frac{π}{2}$<A-B≤π时,cos(B-A)<0,
∴$\frac{1}{tan2A}$-$\frac{1}{tan2B}$<0,∴$\frac{1}{tan2A}$<$\frac{1}{tan2B}$;
则$\frac{1}{tan2A}$>$\frac{1}{tan2B}$;,故③错误;
④cos2A-cos2B=$\frac{1}{2}$(2cos2A-2cos2B)
=$\frac{1}{2}$[(2cos2A-1)-(2cos2B-1)]
=(cos2A-cos2B)
=$\frac{1}{2}$×(-2)×sin(A+B)×sin(A-B)
=-sin(A+B)sin(A-B),
∵A>B,∴0<A-B<π
∵0<A+B<π,∴sin(A+B)>0,
∴cos2A-cos2B<0,cos2A<cos2B.故④正确;
⑤tan$\frac{A}{2}$-tan$\frac{B}{2}$=tan$\frac{A}{2}$-tan(-$\frac{B}{2}$)=$\frac{sin\frac{A-B}{2}}{cos\frac{A}{2}cos(-\frac{B}{2})}$,
∵0<$\frac{B-A}{2}$<$\frac{π}{2}$,0<$\frac{B}{2}$≤$\frac{π}{2}$,
∴tan$\frac{A}{2}$-tan$\frac{B}{2}$<0,
∴tan$\frac{A}{2}$<tan$\frac{B}{2}$;
故⑤正确,
故正确命题的序号是:①②④⑤,
故答案为:①②④⑤
点评 本题考查命题真假的判断,解题时要认真审题,注意正弦定理、三角函数加法定理、倍角公式等知识的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {0,1,3} | D. | B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
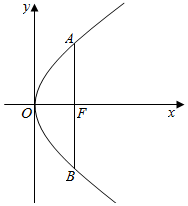 如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.
如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,则n⊥β | B. | 若m⊥n,n?α,则n⊥β | C. | 若m∥n,则n∥β | D. | 若m∥n,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,lg6] | B. | (-∞,3lg2] | C. | [lg6,+∞) | D. | [3lg2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com