
分析 (Ⅰ)求出f(x)的导数,由f′(2)=0,求出a的值,从而求出函数的单调区间;(Ⅱ)根据二次函数的性质求出k的范围即可.
解答 解:(Ⅰ)因为$f(x)=-6ln(ax+2)+\frac{1}{2}{x^2}$,
所以$f'(x)=-6•\frac{a}{ax+2}+x$
由f′(2)=0,可得 a=2,
经检验a=2时,函数f(x)在x=2处取得极值,
$f(x)=-6ln(2x+2)+\frac{1}{2}{x^2}$,${f^'}(x)=\frac{-6}{x+1}+x=\frac{{{x^2}+x-6}}{x+1}=\frac{(x+3)(x-2)}{x+1}$
而函数f(x)的定义域为(-1,+∞),
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-1,2) | 2 | (2,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
点评 本题考查了函数的单调性问题,考查导数的应用以及二次函数的性质,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=$({x^2}{)^{\frac{1}{2}}}$,g(x)=$({x^{\frac{1}{2}}}{)^2}$ | B. | f(x)=$\frac{x^2-9}{x+3}$,g(x)=x-3 | ||
| C. | f(x)=${log_2}{x^2}$,g(x)=2log2x | D. | f(x)=x,g(x)=lg10x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,0)∪(1,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
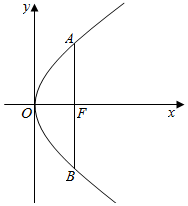 如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.
如图所示,已知抛物线C:y2=2px(p>0)的焦点为F,过点F垂直于x轴的直线与抛物线C相交于A,B两点,抛物线C在A,B两点处的切线及直线AB所围成的三角形面积为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点F1,F2分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点A是下顶点,抛物线C2:y=x2-1与x轴交于点F1,F2,与y轴交于点B,且点B是线段OA的中点,点N为抛物线上C2的一动点,过点N作抛物线C2的切线交椭圆C1于P,Q两点.
如图,点F1,F2分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点A是下顶点,抛物线C2:y=x2-1与x轴交于点F1,F2,与y轴交于点B,且点B是线段OA的中点,点N为抛物线上C2的一动点,过点N作抛物线C2的切线交椭圆C1于P,Q两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥n,则n⊥β | B. | 若m⊥n,n?α,则n⊥β | C. | 若m∥n,则n∥β | D. | 若m∥n,则n⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60 | B. | 90 | C. | 150 | D. | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com